2. Concepts de la cartographie
Résumé de section
-
Pour comprendre des termes liés aux cartes : les coordonnées, les systèmes de projection, les échelles...
Temps de lecture : 50 min
-
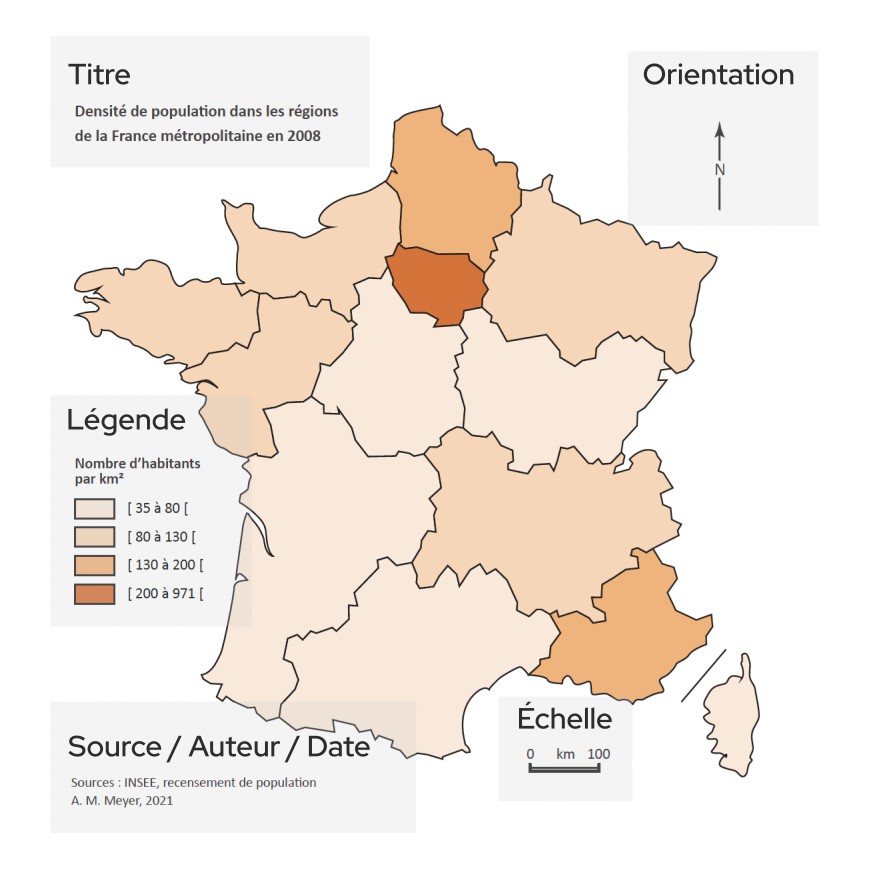
Une carte comporte normalement :
- Un titre ;
- Une échelle ;
- Une légende ;
- Un auteur et éventuellement les sources des données ;
- Une date de publication.
L'orientation (indication du nord) est parfois aussi présente sur les cartes. Outre ces éléments, une carte est un document dont la réalisation obéit à certains concepts que nous allons aborder maintenant.
-
Latitude et longitude
Pour déterminer la position exacte d'un point sur Terre, il faut combiner sa latitude et sa longitude.
La latitude
C'est une valeur angulaire d'un point de la Terre mesurée depuis l'équateur (le parallèle de référence). Cette valeur varie entre 0° et 90° vers les pôles nord et sud.
Ex : la latitude de Bordeaux est 45° nord.
La longitude
C'est l'autre valeur angulaire, variant d'est en ouest entre 0° et 180° autour du méridien de Greenwich (le méridien de référence).
Ex : la longitude de Nice est 7° est.
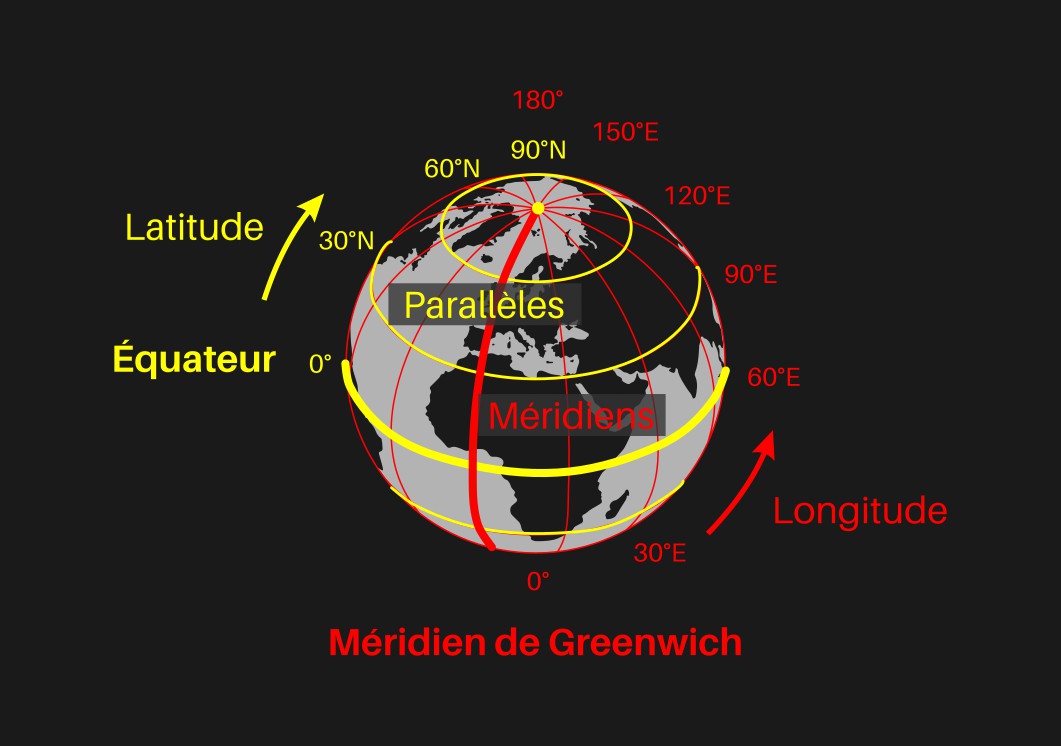
Illustration des latitudes / parallèles, longitudes / méridiens, réadaptée de Latitude and Longitude of the Earth, Djexplo, CC0, via Wikimedia Commons
-
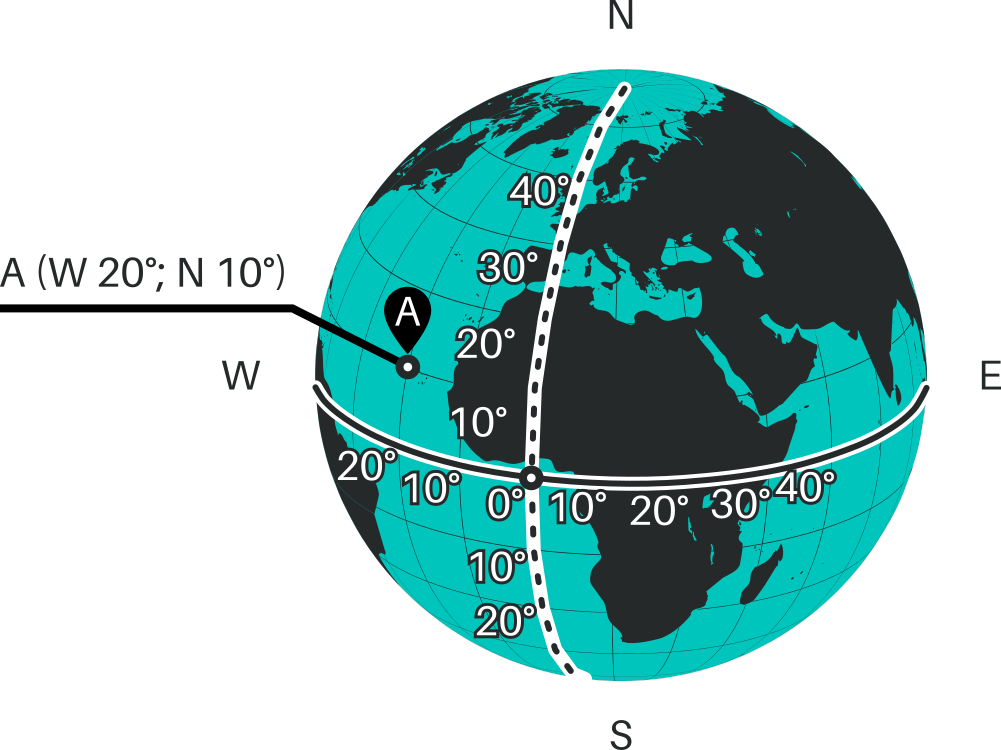
Exemple
Pour déterminer les coordonnées géographiques du point A, nous nous basons sur le point d'intersection entre l'équateur et le méridien de Greenwich.
À partir de ce point de référence, nous regardons sur la grille à quel degré la longitude du point A se trouve. Elle se trouve à 20° ouest (West) du point de référence.
On fait la même chose pour la latitude. On voit qu'elle se trouve à 10° nord du point de référence.
On peut ainsi écrire les coordonnées géographiques du point A (W 20°;N 10°)
NB : Pour localiser un point de façon plus précise, on peut diviser les degrés en minutes et en secondes. On écrit les minutes à la suite des degrés, en ajoutant une apostrophe. On écrit les secondes à la suite des minutes, en ajoutant deux apostrophes.
Ex : W 20°0’21’’ / N 10°41’42’’
- W (West), N (Nord) = Direction
- ° = Degrés
- ' = Minutes
- " = Secondes
-
Les systèmes de projection
La projection cartographique est une opération mathématique qui permet de représenter sur une carte en 2 dimensions tout ou partie de la Terre qui est quant à elle une figure en 3 dimensions.
La projection tient compte de la forme de la Terre et d’un système de coordonnées. Ainsi la Terre est projetée selon une figure qui sera ensuite "mise à plat". Ci-dessous quelques illustrations tirées de la vidéo Projection cartographique des Éditions Larousse.
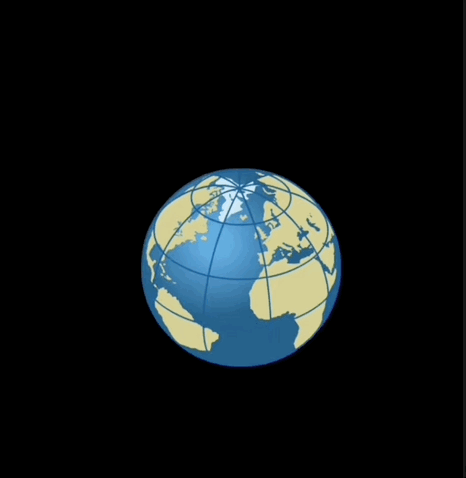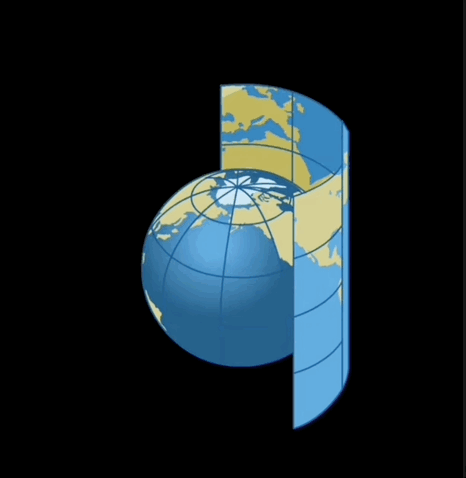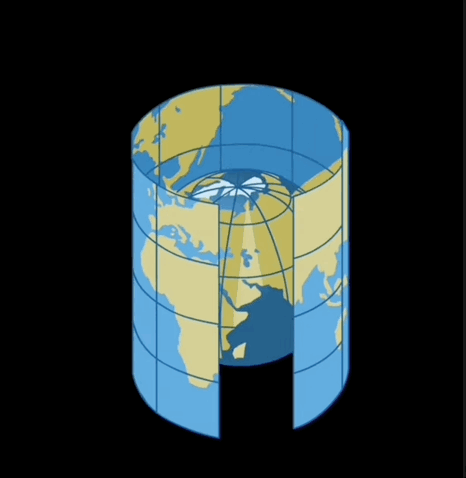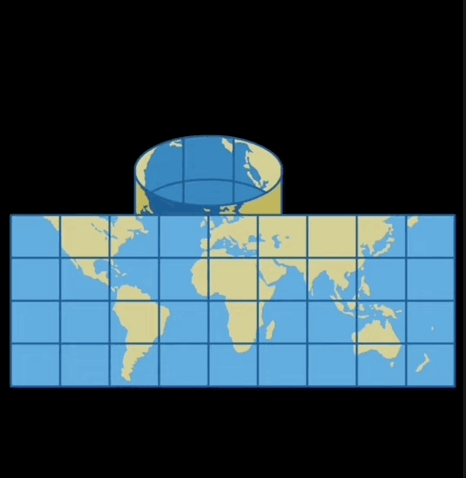
Projection cylindrique
Projection conique
Projection azimutale
La vidéo ci-dessous présente les grands types de projection (cylindriques, azimutales, coniques) ainsi que les différentes représentations de la Terre et les usages qui en découlent.
Vidéo sur les projections cartographiques réalisée par le consortium ImaGEO pour le serious game Madmaps.
-
Le langage cartographique (sémiologie des cartes)
Les bases du langage cartographique ont été posées par Jacques Bertin en 1967 dans "La sémiologie graphique".
Les cartes expriment des informations de manière graphique. Connaître les règles de sémiologie graphique permet donc de mieux lire les cartes.
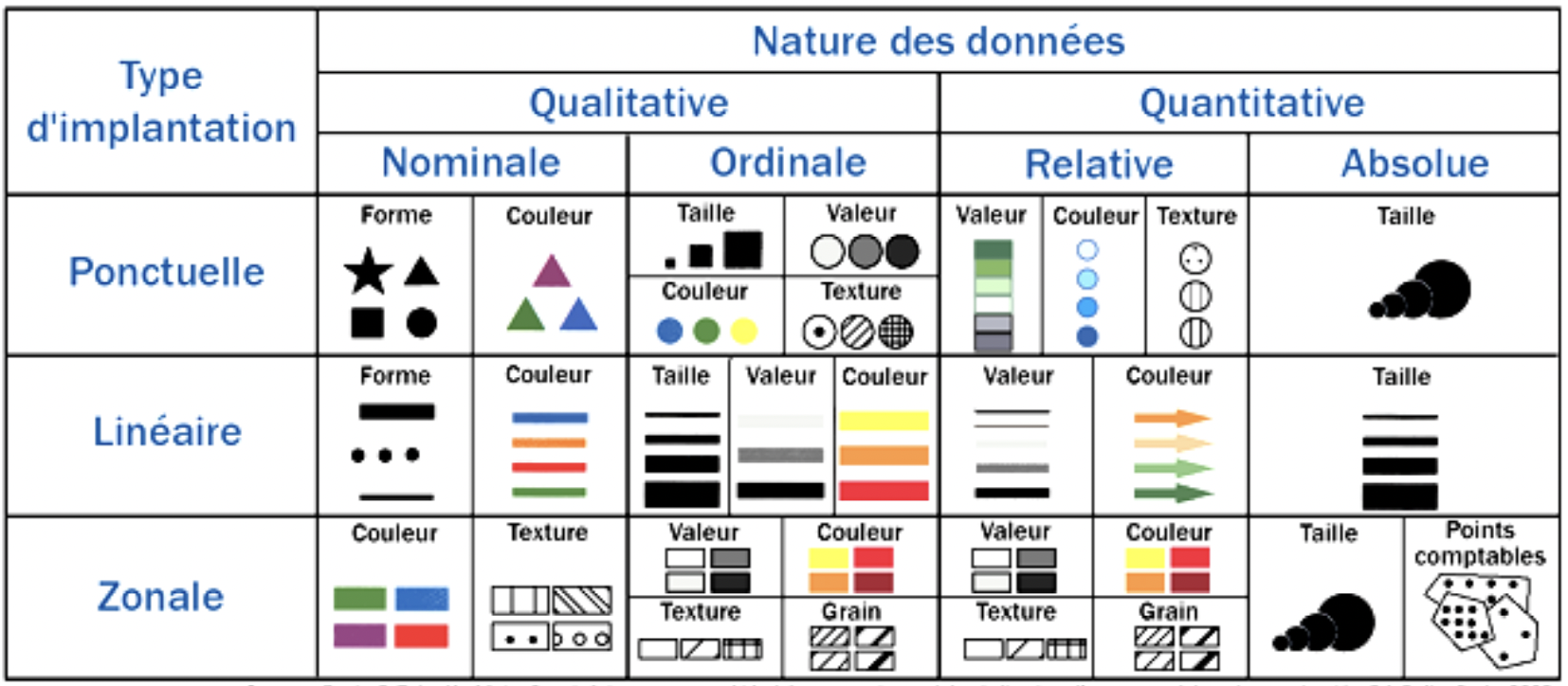
C. Zanin et M.-L. Tremelo (2003), Savoir faire une carte. Aide à la conception et à la réalisation d'une carte thématique. Belin, Paris.
Pour les comprendre, il faut cependant garder à l’esprit que les cartes ne montrent pas une réalité objective du monde. Elles portent en elles une forme de discours qui résulte de choix et d’intentions.
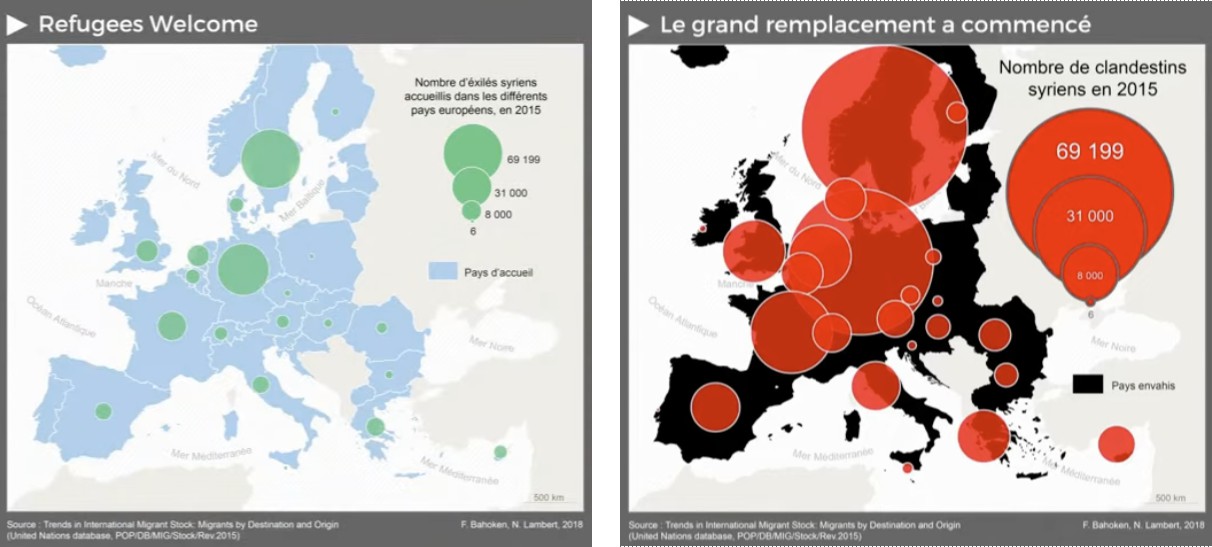
Les deux cartes ci-contre ont été construites avec exactement les mêmes données. On observe pourtant qu'elles véhiculent des messages opposés :
- Un message accueillant à gauche ; couleurs douces renvoyant à un sentiment de paix et de sérénité, lexique connoté ("accueil", "réfugiés", "exilés")...
- Un message de rejet à droite ; couleurs vives et contrastées renvoyant à un sentiment de peur, lexique connoté ("grand remplacement", "clandestins"), exagération de la taille des cercles...
La vidéo ci-dessous explique comment la cartographie obéit ainsi à des codes de langage précis (couleurs, formes, tailles, etc.) et largement partagés… tout en étant manipulables. Elle interroge ainsi la notion de "bonne carte" et définit ce qu’est le métier de cartographe aujourd’hui.
Vidéo sur la sémiologie graphique réalisée par le consortium ImaGEO pour le serious game Madmaps.
-
Les échelles
Autre concept majeur de la cartographie, l’échelle est le rapport entre une longueur réelle sur le terrain et sa représentation cartographique. Comme il s'agit d'un rapport, l'échelle s'écrit sous la forme d'une fraction, par exemple 1:100 000 (ou 1/100 000). Cela signifie que 1 cm sur la carte équivaut à 100 000 cm sur le terrain (soit 1 km).
km hm dam m dm cm 1 0 0 0 0 0 Sur une carte, l'échelle peut apparaître de manière numérique ou graphique.
Échelle numérique Échelle graphique 1 : 1 000 000
1 cm sur la carte = 10 km
1 : 100 000
1 cm sur la carte = 1 km
1 : 50 000
1 cm sur la carte = 500 m
Exemples d'échelles numériques et graphiquesL’échelle graphique est le moyen le plus sûr pour apprécier les distances sur la carte. De plus, lors de l’agrandissement ou la réduction d’une carte, l’échelle graphique suit la déformation, alors qu’il faudra déterminer de nouveau l’échelle numérique.
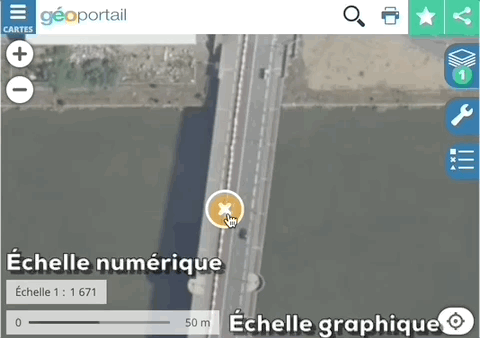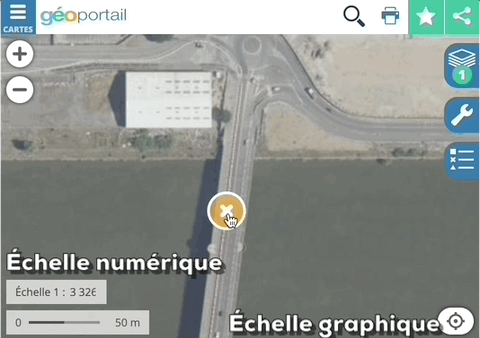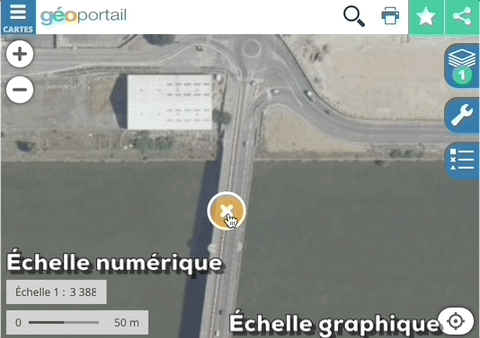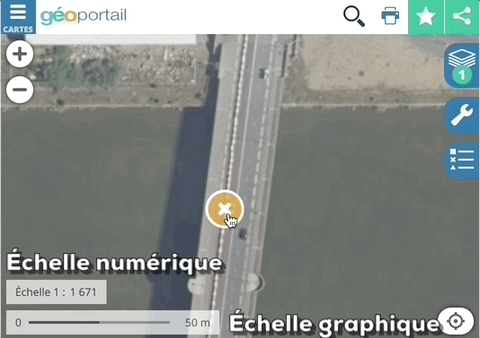
L'échelle numérique est recalculée durant l'agrandissement / rétrécissement et l'échelle graphique se déforme. Image extraite de géoportail.
-
Plus l'échelle est petite, plus l'espace est grand
On peut prendre la comparaison avec un avion qui décolle, notre vision change à mesure que l’avion prend de la hauteur, on voit plus loin, mais avec moins de précision.
Les grandes échelles représentent de façon détaillée un espace restreint. On parle de plan pour des échelles au-delà de 1:20 000 (cadastre, plan de ville).
Les échelles moyennes sont comprises entre 1:50 000 et 1:500 000 (environs d’une ville, départements, régions).
Les petites échelles débutent à partir de 1:500 000 (régions, États), et on parle de très petite échelle à partir de 1:10 000 000 (continents, planisphères).
Ci-dessous quelques exemples issus de Géoportail.
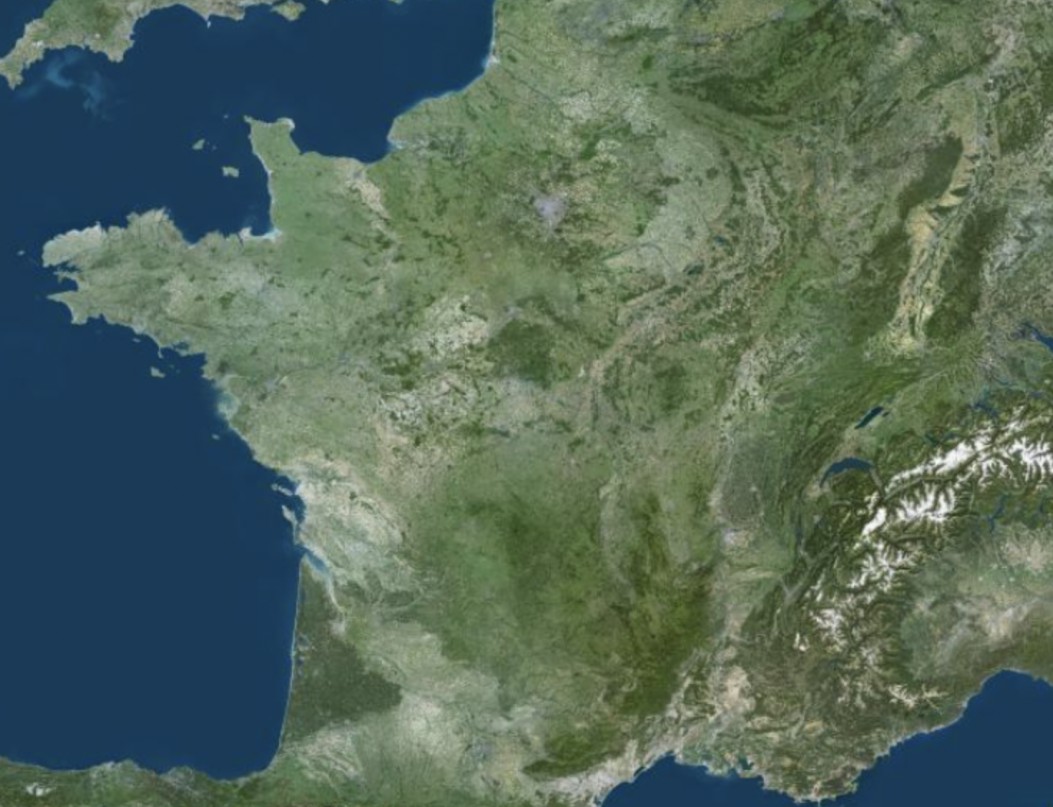
Exemple de petite échelle
(1:800 000)
Exemple de moyenne échelle
(1:180 000)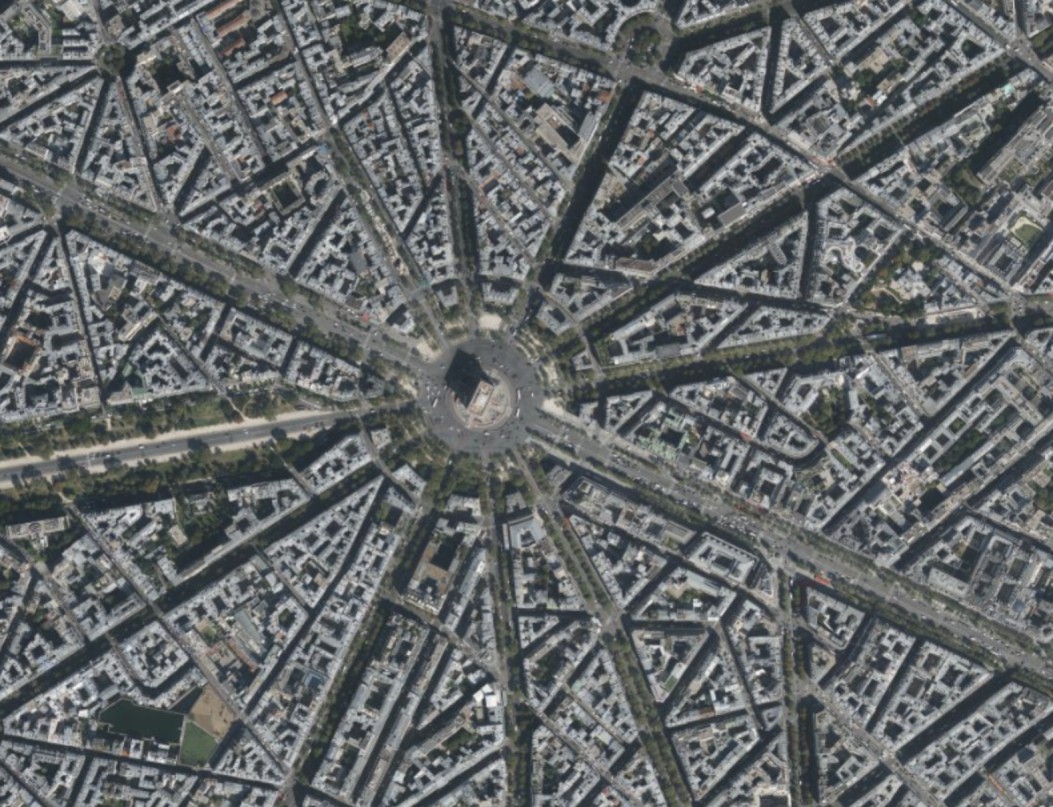
Exemple de grande échelle
(1:10 000) -
Sur les cartes anciennes, l’échelle, peu précise, servait souvent d’élément décoratif. Avant l’uniformisation des unités de mesure, chaque contrée possédait ses mesures, et il y avait donc souvent plusieurs barres d’échelle graphiques. Sur l’exemple ci-dessous qui représente un espace de l’actuelle Estonie, on trouve l’échelle en verstes (mesure itinéraire de Russie), mais aussi en miles de Livonie, et en miles d’Allemagne.
Extrait de la carte : Der Pernausche Kreis (Le cercle de Pernau). 1797. 1886 Université Bordeaux Montaigne
De nos jours on trouve toujours des cartes avec deux barres d'échelle (OpenStreetMap par exemple), une pour le système métrique (kilomètres) et une autre pour le système anglo-saxon (miles).
-
Calcul par comparaison avec une carte d’échelle connue
Si l'on a une carte qui ne comporte aucune échelle, une solution pour la retrouver est de s'appuyer sur une autre carte qui elle en a une. La méthode reste la même que celle vue précédemment.
On mesure sur notre carte la distance en cm entre 2 points identifiés. Par exemple ici, on mesure 6,7 cm sur la carte entre 2 points (Ussel et Eygurande).
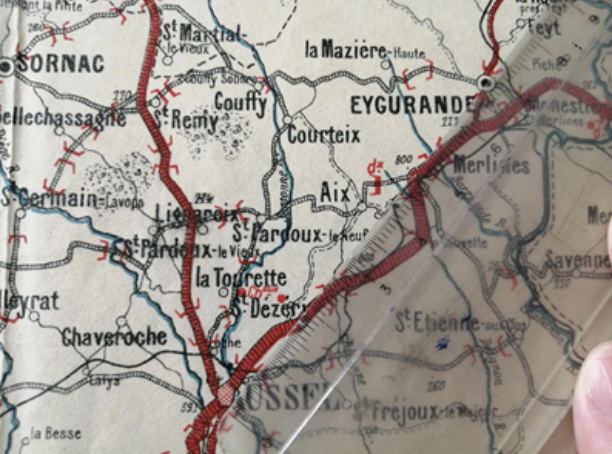
Sur une carte d’échelle connue ou un outil mesurant les distances (Google Earth par exemple), on mesure la distance entre ces deux mêmes points identifiés. Ici par exemple, on mesure sur Google Earth la distance entre Ussel et Eygurande et l'on trouve 16,5 km.
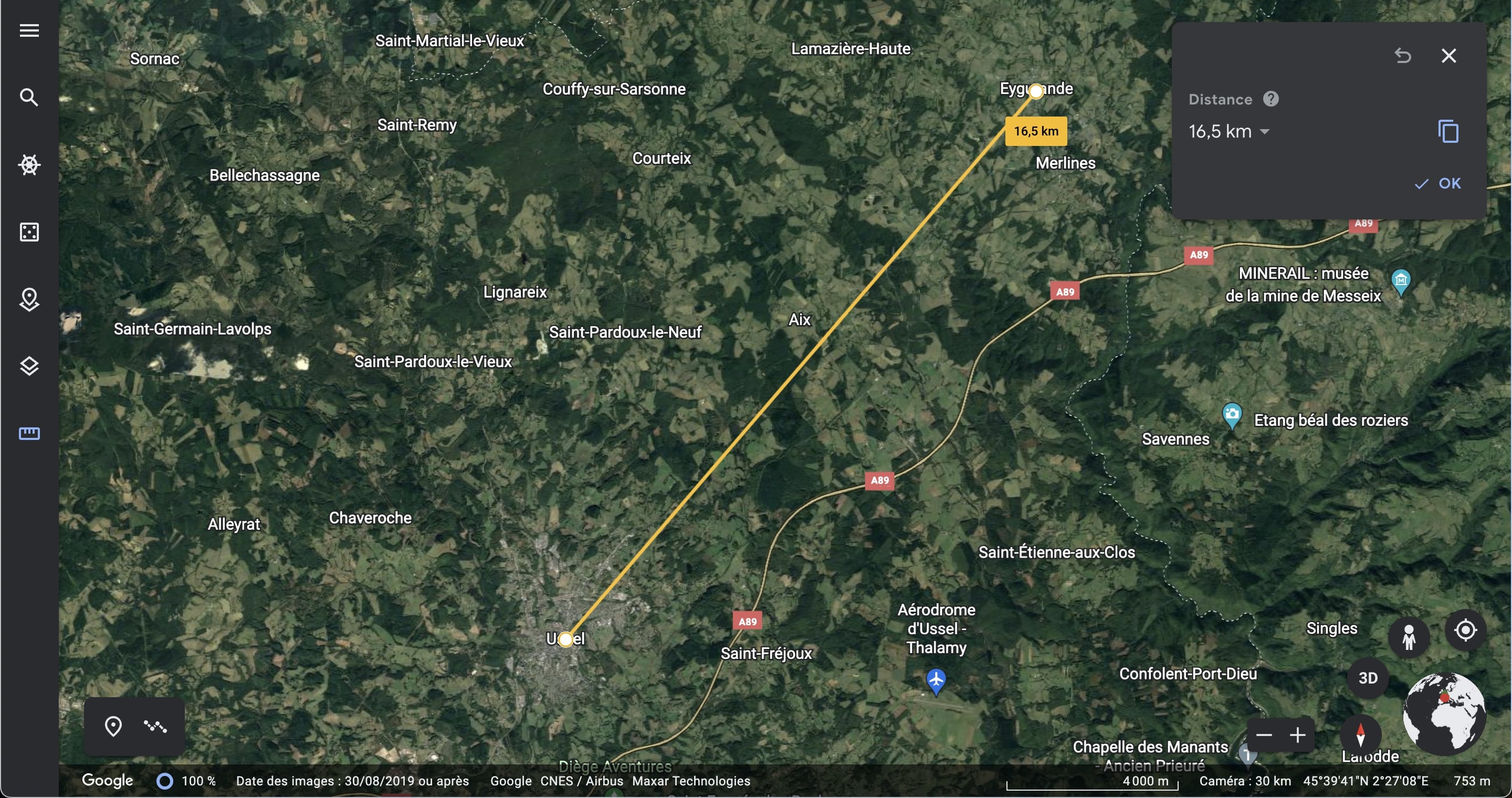
On convertit cette distance en cm : 16,5 km = 1 650 000 cm. On en conclut donc que 6,7 cm sur notre carte correspond à 1 650 000 cm dans la réalité.
6,7 cm sur la carte
1 650 000 cm en réalité
Enfin, on réalise un produit en croix pour calculer combien 1 cm sur la carte représente de cm sur le terrain :
- (1 × 1 600 000) ÷ 6,7 = 247 373
- 1 cm sur la carte = 238 806 cm dans la réalité
En arrondissant, on trouve alors l'échelle 1:250 000.
-