Résumé de section

    • Nous avons vu qu'un élément observé peut être positionné à la surface de la Terre à l'aide de coordonnées. Il s'agit souvent d'un doublet (latitude/longitude; est/nord) ou d'un triplet (latitude/longitude/hauteur ellipsoïdale; est/nord/altitude).

      Pour pouvoir les exploiter, il faut savoir dans quel système de référence de coordonnées elles sont exprimées. C'est une métadonnée d'importance.

      Il existe deux grands types:  

      • les systèmes géodésiques (aussi appelés systèmes de référence de coordonnées géographiques)
      • les systèmes de référence cartographiques (aussi appelés projections)

      La vidéo ci-dessous présente en 3 minutes les problématiques liées aux systèmes de référence et plus particulièrement les projections cartographiques.

    • Pourquoi existe-t-il deux systèmes ?

      La forme de la Terre se rapproche d'une sphère aplatie aux pôles, il est simple de localiser un point à sa surface à l'aide d'angles. Ainsi la latitude était mesurée avec précision dès l'Antiquité. La mesure de la longitude devra attendre les progrès de l'horlogerie aux XVIIe et XVIIIe siècles. C'est un système encore couramment utilisé pour la navigation aérienne ou maritime et par les systèmes GNSS. Mais il n'est pas pratique de mesurer une distance ou une surface sur un globe. C'est plus commode de faire des mesures sur une surface plane posée sur une table. Une carte sur du papier ou du vélin peut être roulée ou pliée, ce qui la rend bien plus pratique qu'une mappemonde. Pour créer une carte, il est nécessaire de projeter la sphère (systèmes géodésiques) sur le plan (systèmes projetés), c'est pourquoi on parle de projection. Pour passer d'un système de référence de coordonnées (géographique ou non) à un autre, on parlera d'une transformation. Les deux types de systèmes coexistent encore à l'heure actuelle et les ordinateurs permettent de passer de l'un à l'autre très simplement.

    • Systèmes géodésiques

      Il s'agit de systèmes où les coordonnées (latitude et longitude) sont des angles formés entre le centre de la Terre, l'Équateur et le premier méridien (ou méridien  de Greenwich). 

      Ces angles sont exprimés en degrés, minutes, secondes ou en degrés décimaux. 

      Ces points sont rattachés à un ellipsoïde de révolution, similaire à une sphère aplatie aux pôles, chargé d'approximer la surface terrestre. 

      Une troisième coordonnée, la hauteur ellipsoïdale est la différence entre le point considéré et l'ellipsoïde. Il ne s'agit pas d'une altitude, elle peut différer de plusieurs dizaines de mètres.

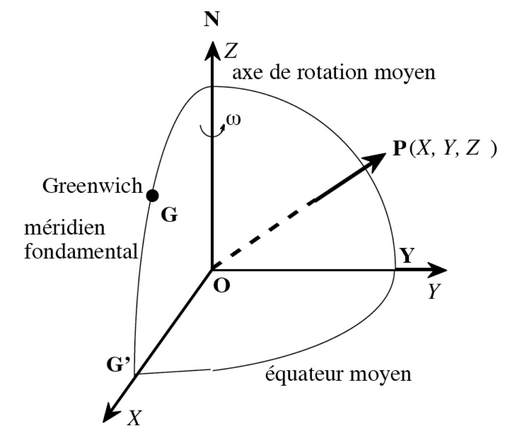      The original uploader was Carlo denis at French Wikipedia., CC BY-SA 3.0, via Wikimedia Commons

      Les systèmes de navigation par satellites utilisent un système géodésique, c'est le cas du GPS américain qui repose sur le WGS 84.

    • Systèmes cartographiques (aussi appelés projections)

      Les systèmes de coordonnées projetées permettent la représentation de points situés à la surface terrestre sur une surface plane. 

      Cette opération, appelée transformation, engendre des déformations. Le travail du cartographe est de choisir la plus adaptée, selon que la carte devra préserver les angles, les distances, les surfaces ou rien de tout cela.

      Projections conformes

      Les projections conformes préservent les angles, facilitant la navigation entre deux points. C'est le cas de la projection Transverse universelle de Mercator (Universal Transverse Mercator ou UTM) par exemple. Cette projection est encore très utilisée puisqu'une variante dédiée aux applications cartographiques web a été créée, la projection Web Mercator. Bien qu'omniprésente sur les services de cartographies en ligne tels qu'OpenStreetMap ou Google Maps, elle n'est pas exempte des défauts de sa grande sœur (voir ci-dessous le passage sur la visualisation des déformations induites par la projection Mercator).

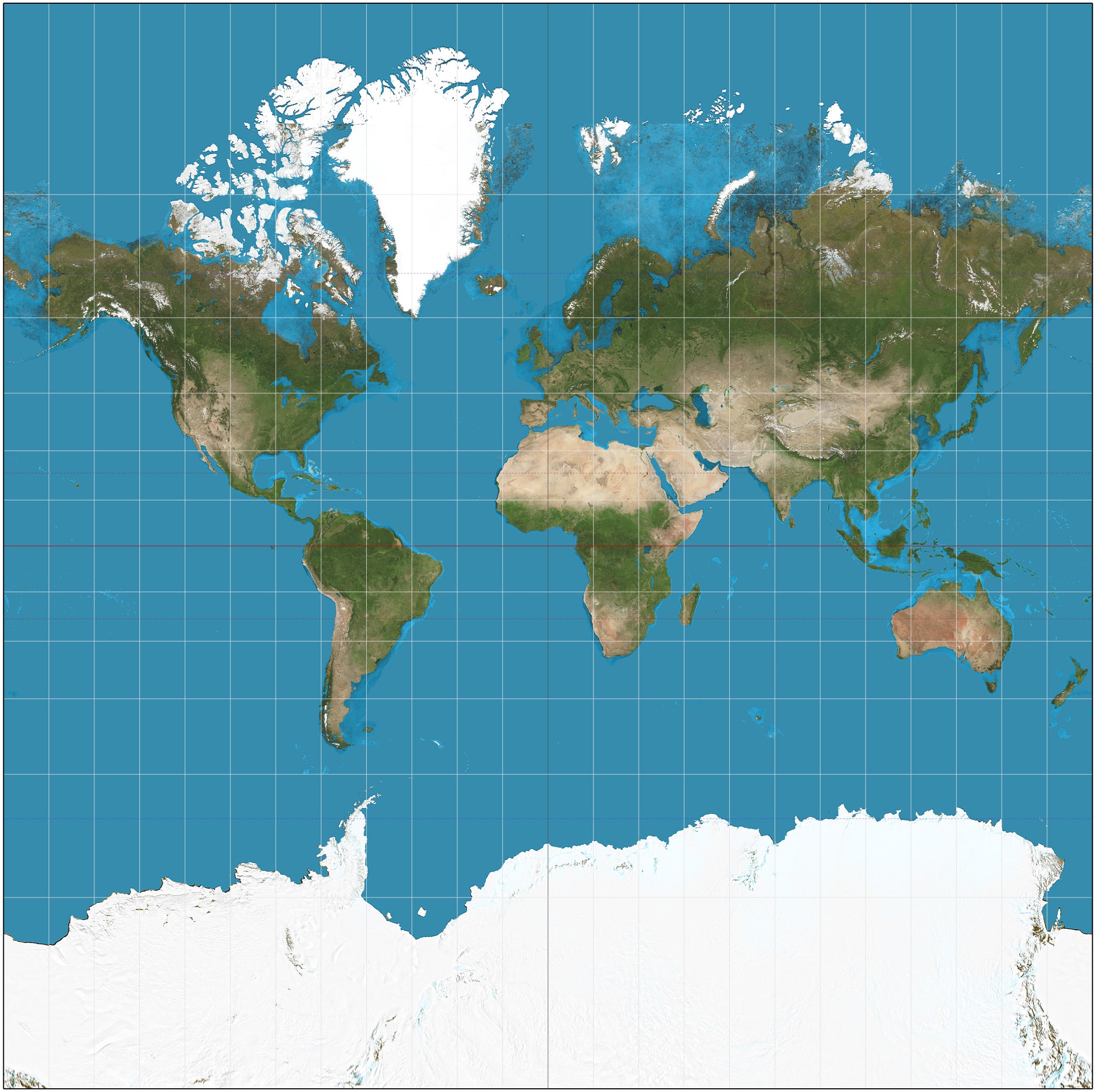      Voir légende.
      Exemple de projection Web Mercator. Strebe, CC BY-SA 4.0, via Wikimedia Commons
      Voir la légende.
      Projection de Peters de la Terre. Mdf, Public domain, via Wikimedia Commons
      Projections équivalentes

      Les projections équivalentes préservent les surfaces, ce qui les rendent utiles pour des comparaisons de densité par exemple. Ainsi, la projection de Gall-Peters montre un Groënland 14 fois plus petit que le continent africain, contrairement à la projection UTM, ce qui correspond à la réalité.

      Projections équidistantes

      Les projections équidistantes préservent les distances mais ne conservent ni les angles ni les surfaces.

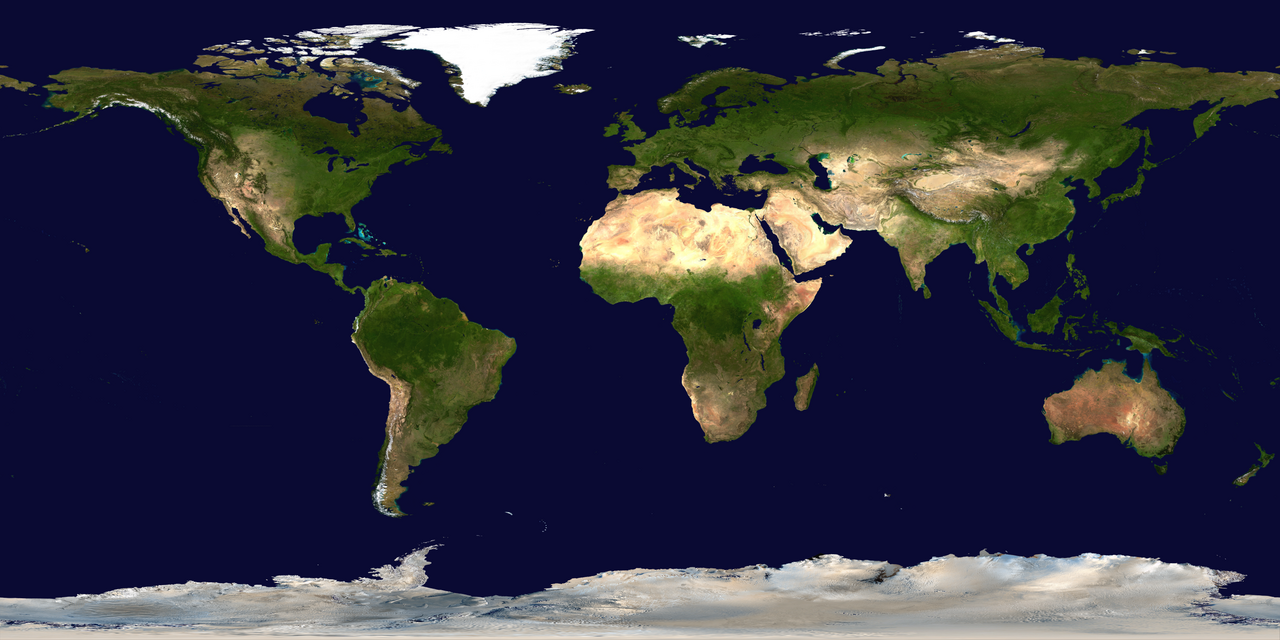      Description dans la légende ci-dessous.
      Projection équirectangulaire de la Terre. NASA
    • Visualiser les déformations avec les indicatrices de Tissot

      Comme nous l'avons vu précédemment, toutes les projections déforment la réalité. Il peut être intéressant de visualiser ces déformations pour mieux s'en rendre compte. C'est ce que permettent les indicatrices de Tissot.

      Les deux images ci-dessous représentent la même chose : des surfaces appelées indicatrices de Tissot. Elles servent à visualiser les déformations produites par une projection. 

      L'image de gauche représente ces indicatrices réparties régulièrement autour du globe. Tous les cercles font la même taille. L'image de droite reprend les mêmes cercles mais sur une carte utilisant la projection universelle transverse de Mercator: les cercles grossissent plus leur latitude augmente (vers les pôles).

      World Map (Canvas) with Tissot’s Indicatrices - Sorami Hisamoto, Observable

      La NASA propose de visualiser les déformations de différentes projections dans cette vidéo de 47 secondes.

      Map Projections Morph - NASA Scientific Visualization Studio, on YouTube

    • Pourquoi la gestion des systèmes de référence de coordonnées peut être problématique ?

      La gestion des systèmes de référence de coordonnées (souvent abrégé avec l'acronyme anglophone CRS) pose généralement des problèmes aux personnes confrontées pour la première fois à des données géographiques et même des utilisateurs chevronnés pourront se faire avoir de temps en temps.

      Croiser des données géographiques ayant des CRS différents (par exemple WGS 84 d'un côté et RGF93/Lambert93 de l'autre) pourra, au mieux, ne retourner aucun résultat ou, dans le pire des cas, retourner un résultat erroné. L'ordinateur exécutera l'algorithme sans se poser de questions, c'est à l'opérateur (c'est-à-dire vous) de prêter attention aux CRS des couches utilisées.

      Les algorithmes fonctionnant avec des distances (ou calculant des surfaces) sont souvent codés pour fonctionner pour des systèmes de coordonnées projetés. Par exemple, un algorithme calculant la distance entre deux points utilisera par défaut la distance euclidienne (le théorème de Pythagore, vous vous souvenez ?) car c'est rapide et peu couteux à réaliser. Par contre, pour des données dans un système géodésique, situant des objets à la surface de la Terre, il faut calculer la distance orthodromique (ou distance du grand cercle). Cette méthode nécessitant de calculer des sinus et des cosinus, il est alors préférable de transformer les coordonnées dans un système de coordonnées planes avant d'effectuer des calculs de distance. La puissance de calcul des ordinateurs ayant fortement progressée, il est possible de calculer la distance orthodromique mais il convient de choisir un algorithme adapté.

    • Comment choisir une projection ?

      Nous avons vu que la transformation de coordonnées géographiques vers un système de référence de coordonnées projetées entraine une déformation. Il convient alors de choisir une projection adaptée au besoin et à la zone représentée.



      Quel est le besoin ?
      • A-t-on besoin de mesurer des angles ? Une projection conforme est préférable.
      • Des distances ? Une projection équidistante sera à privilégier.
      • De calculer des aires ou des densités ? L'utilisation d'une projection équivalente est recommandée.


      Quelle zone est représentée ?
      • Pour les zones équatoriales et tropicales, les projections cylindriques comme la projection UTM sont adaptées.
      • Pour les zones de latitudes moyennes (France/Europe par exemple), les projections coniques sont fréquemment utilisées.
      • Pour les hautes latitudes (Pôles et cercle arctique), il est préférable d'utiliser une projection azimutale.


      Une bonne piste pour trouver une projection adaptée à une zone d'études est de regarder les projections légales. Par exemple, l'IGN fournit des projections légales pour la France métropolitaines et les départements, régions et collectivités d'outre-mer. Ces projections planes légales sont définies dans l'article 3 de l'Arrêté du 5 mars 2019 portant application du décret n° 2000-1276 du 26 décembre 2000.

    • Pour des raisons historiques, esthétiques ou de représentation, d'autres projections peuvent être choisies (projections de Fuller, de Bonne ou Goode par exemple).

      Un cartographe qui travaille sur les océans mondiaux saura utiliser à son avantage la superbe projection de Spilhaus.


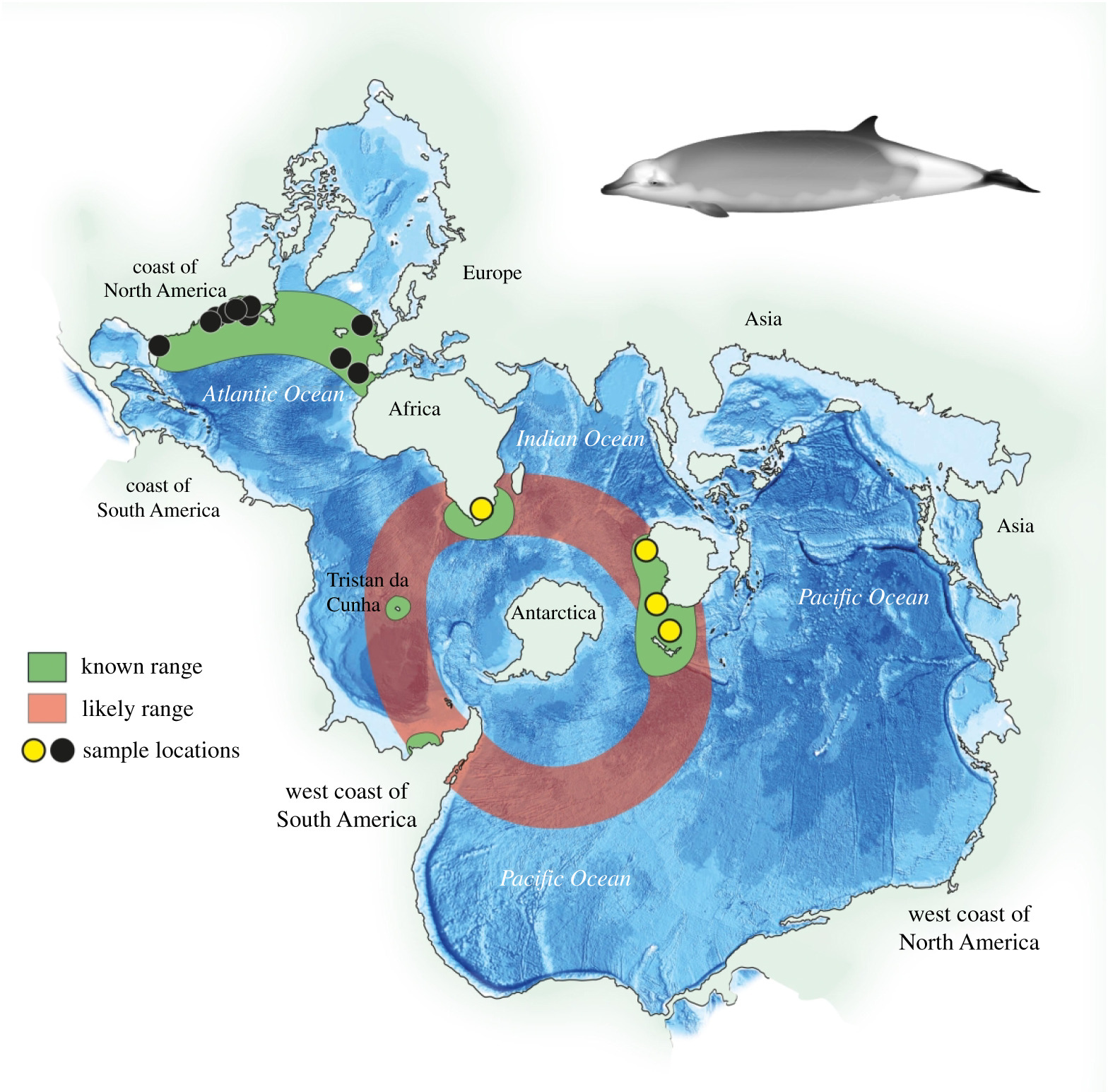      Description ci-dessous.
      Carte d'échantillonnage de baleines à bec utilisant la projection de Splihaus.
      Source: Vivian Ward, CC BY-SA 4.0, via Wikimedia Commons
    • Catalogues

      Les déformations locales de la surface terrestre, les progrès de la technique et d'autres facteurs font que plusieurs milliers de systèmes de références de coordonnées existent. Pour s'y retrouver, des catalogues (ou registres) ont été créés.

      Ces catalogues associent la définition d'un système de référence de coordonnées et un code.

      Ce code est constitué en deux parties séparées par deux points :, à gauche la référence du catalogue (EPSG,IGNF,ESRI) et à droite, le code de la projection dans ce catalogue (respectivement 2154, LAMB93, 102110).

      Ainsi EPSG:2154, IGNF:LAMB93 et ESRI:102110 référencent tous trois la projection RGF93/Lambert93 mais dans 3 catalogues différents.

      Par exemple, la définition WGS84 est associé au code EPSG:4326 alors que sa description en Well-Known Text est la suivante:

                GEOGCRS["WGS 84",
                    ENSEMBLE["World Geodetic System 1984 ensemble",
                        MEMBER["World Geodetic System 1984 (Transit)"],
                        MEMBER["World Geodetic System 1984 (G730)"],
                        MEMBER["World Geodetic System 1984 (G873)"],
                        MEMBER["World Geodetic System 1984 (G1150)"],
                        MEMBER["World Geodetic System 1984 (G1674)"],
                        MEMBER["World Geodetic System 1984 (G1762)"],
                        MEMBER["World Geodetic System 1984 (G2139)"],
                        ELLIPSOID["WGS 84",6378137,298.257223563,
                            LENGTHUNIT["metre",1]],
                        ENSEMBLEACCURACY[2.0]],
                    PRIMEM["Greenwich",0,
                        ANGLEUNIT["degree",0.0174532925199433]],
                    CS[ellipsoidal,2],
                        AXIS["geodetic latitude (Lat)",north,
                            ORDER[1],
                            ANGLEUNIT["degree",0.0174532925199433]],
                        AXIS["geodetic longitude (Lon)",east,
                            ORDER[2],
                            ANGLEUNIT["degree",0.0174532925199433]],
                    USAGE[
                        SCOPE["Horizontal component of 3D system."],
                        AREA["World."],
                        BBOX[-90,-180,90,180]],
                    ID["EPSG",4326]]

       

      EPSG:4326 est plus court et facile à se rappeler, n'est-ce pas ?

      Une même projection pourra avoir plusieurs codes si elle est référencée dans plusieurs catalogues. Ainsi le RGF93/Lambert93 (projection légale en France métropolitaine) correspond aux codes EPSG:2154 et IGNF:LAMB93

      Les outils SIG permettent pour la plupart de transformer vos données d'un système à un autre. Choisissez la projection la plus adaptée à votre zone d'étude et à votre besoin et transformez toutes vos données dans ce système. À moins de travailler à l'échelle mondiale, il est recommandé de travailler avec des systèmes projetés.

      Important: pour croiser des données de manière géographique, il est primordial que les jeux de données soient dans le même système de référence.

      Dans l'exemple ci-dessous tiré de la fenêtre de sélection d'un système de référence de coordonnées de QGIS, il est possible de voir :

      • Dans l'encadré vert, la fenêtre de recherche d'un CRS, ici autour du Lambert93.
      • Dans l'encadré bleu, les CRS disponibles sont regroupés par familles (géocentriques, géographiques, projeté) et en sous-famille. Dans l'exemple, il est possible de voir les sous-familles de projection: Mercator, Orthographique, Lambert conique conforme, etc.
      • Dans l'encadré violet, la description textuelle du RGF93/Lambert93.
      • Dans l'encadré rouge, l'emprise du système de référence de coordonnées (dans l'exemple centré sur la France métropolitaine).

       

       

    • En résumé, pour éviter les écueils
      1. Choisir un système de coordonnées adapté :
        1. à la zone d'étude, à jour si possible
        2. au besoin: a-t-on besoin de calculer des distances ou des surfaces/densités ?
      2. Vérifier les CRS des jeux de données mobilisés et les transformer vers le CRS sélectionné si nécessaire. Tous les logiciels SIG proposent des outils de transformation qui permettent de passer d'un CRS à un autre.
      3. Avant d'utiliser un outil, essayer de savoir s'il fonctionne avec des coordonnées projetées (le cas général) ou non.

      Les sites Spatial Reference et espg.io permettent de rechercher des informations sur un CRS à partir de son code ou de son nom.

    • Systèmes de référence de coordonnées usuels


      France
      Zone Nom Code
      France métropolitaine Lambert-93 IGNF:RGF93LAMB93
      Coniques conformes zone 1 à 9 RGF93CC42 à RGF93CC50
      Antilles françaises Universal transverse Mercator fuseau 20 nord IGNF:RGAF09UTM20
      Guyane Universal transverse Mercator fuseau 22 nord IGNF:RGFG95UTM22
      La Réunion Universal transverse Mercator fuseau 40 sud IGNF:RGR92UTM40S
      Mayotte Universal transverse Mercator fuseau 38 sud IGNF:RGM04UTM38S
    • Europe
      ETRS89-extended / LAEA Europe : projection utilisée pour les données géographiques Eurostat de la Commission Européenne.
      Code EPSG:3035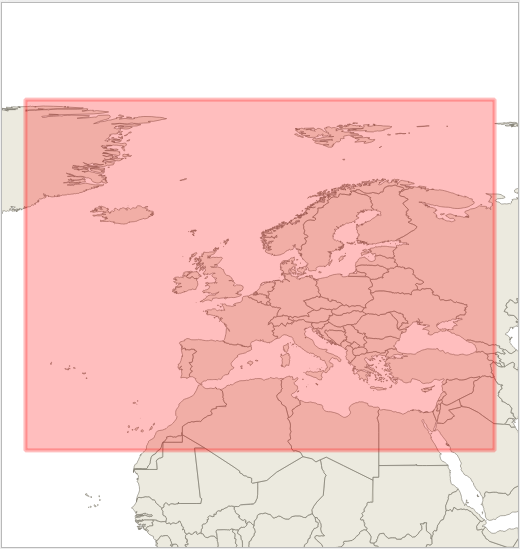


      Monde

      WGS84: système de référence de coordonnées géographiques utilisés par le système GPS.
      Code EPSG:4326

      WGS 84 / Pseudo-Mercator -- Spherical Mercator: projection utilisée par les fonds de cartes web (OpenStreetMap, Google maps, etc.).
      Code ESPG:3857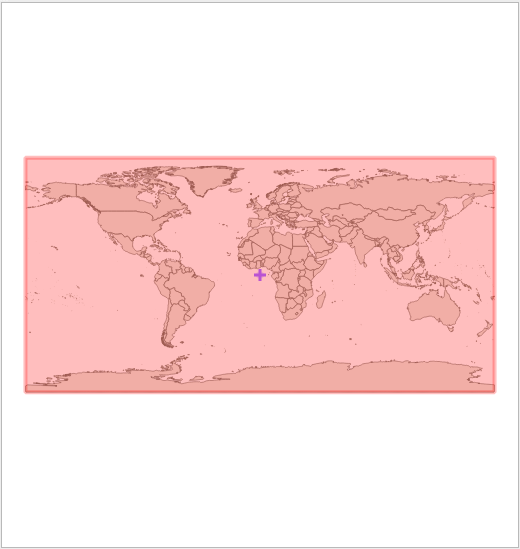