Résumé de section

  • Replier Déplier

    Synopsis

    Tout replier Tout déplier

    L'utilisation des données géospatiales connaît actuellement une croissance considérable. Elle joue un rôle de plus en plus important dans les domaines comme les services publics, l'environnement, l'urbanisme, la recherche, la gestion des ressources naturelles, la santé, l'administration des biens foncier, les réseaux de transport et d'énergie, etc.

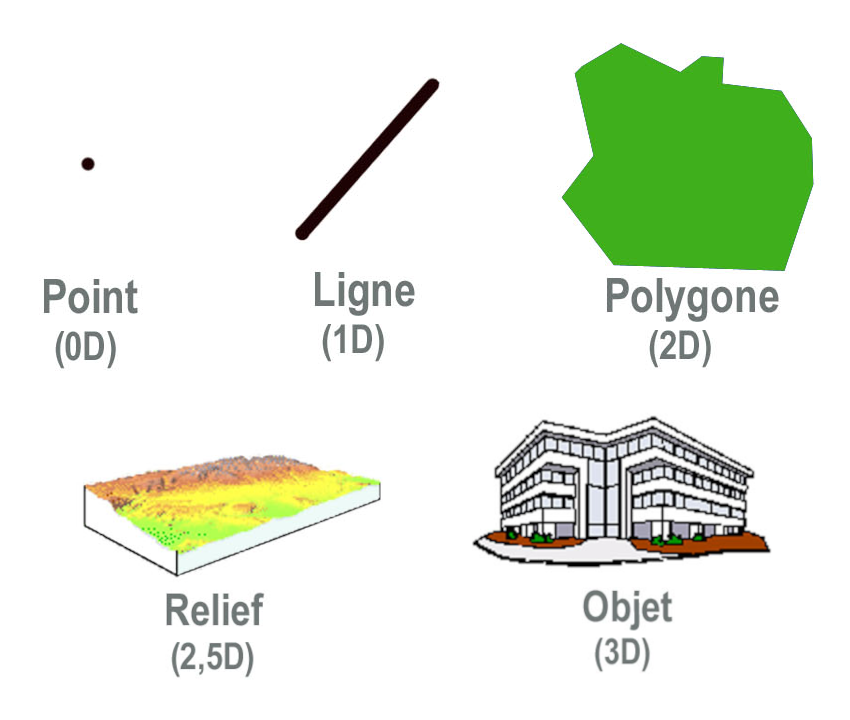
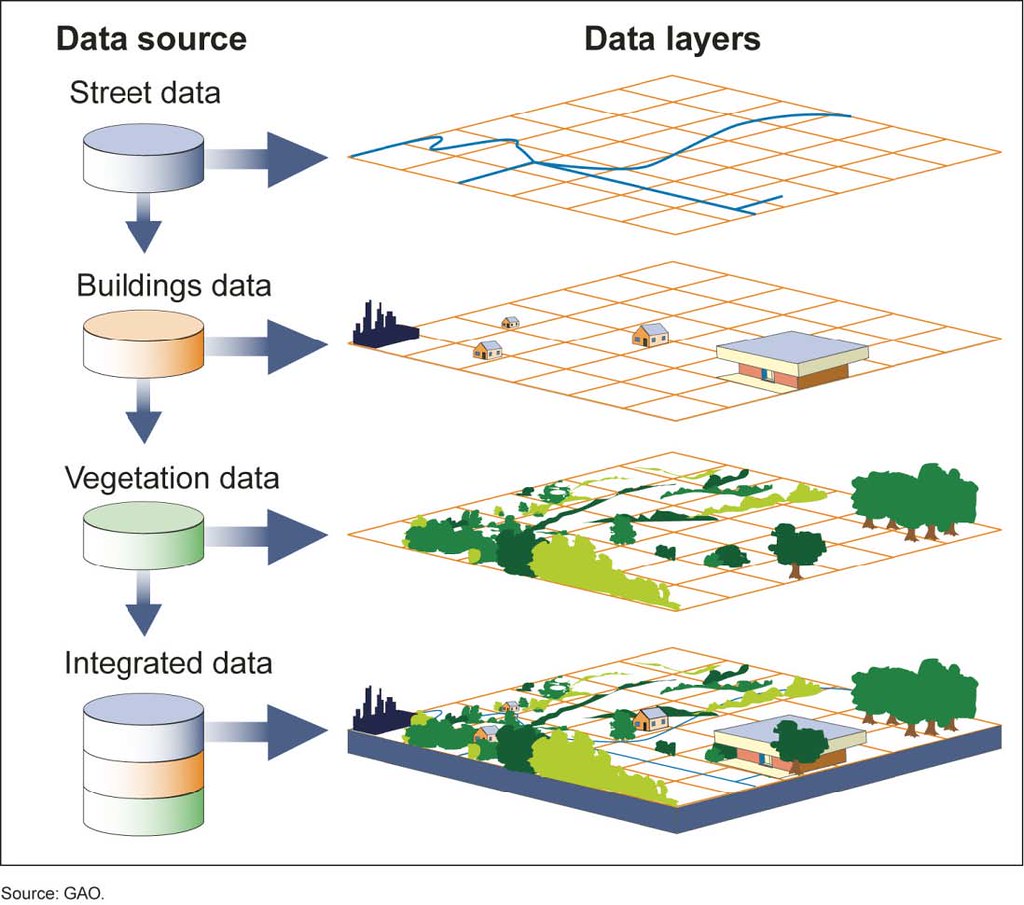
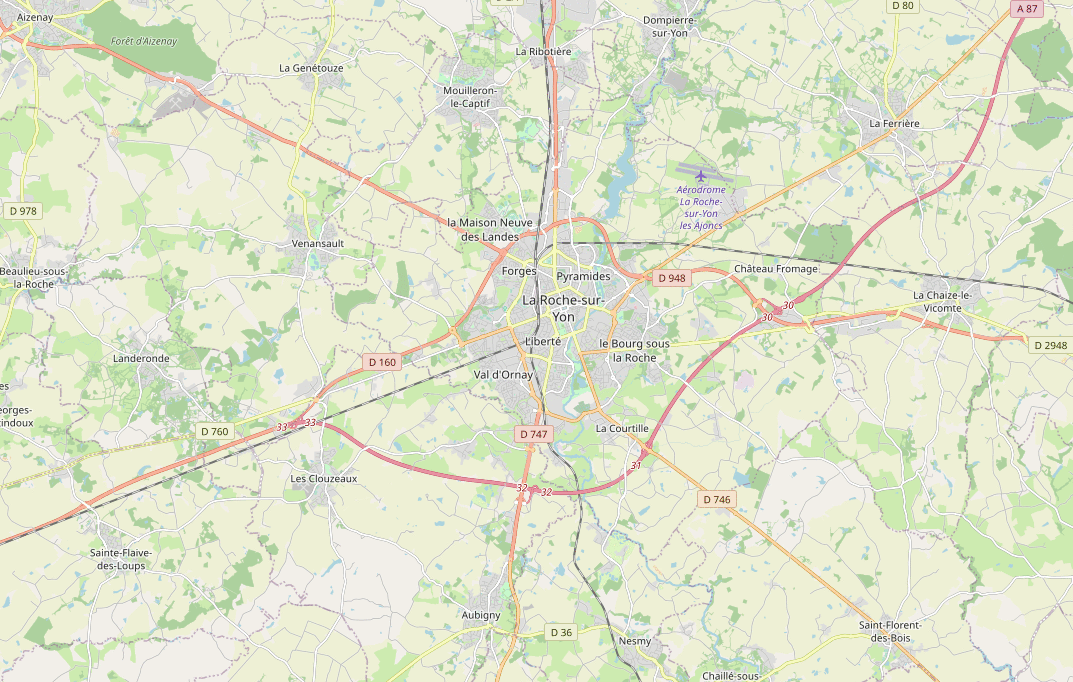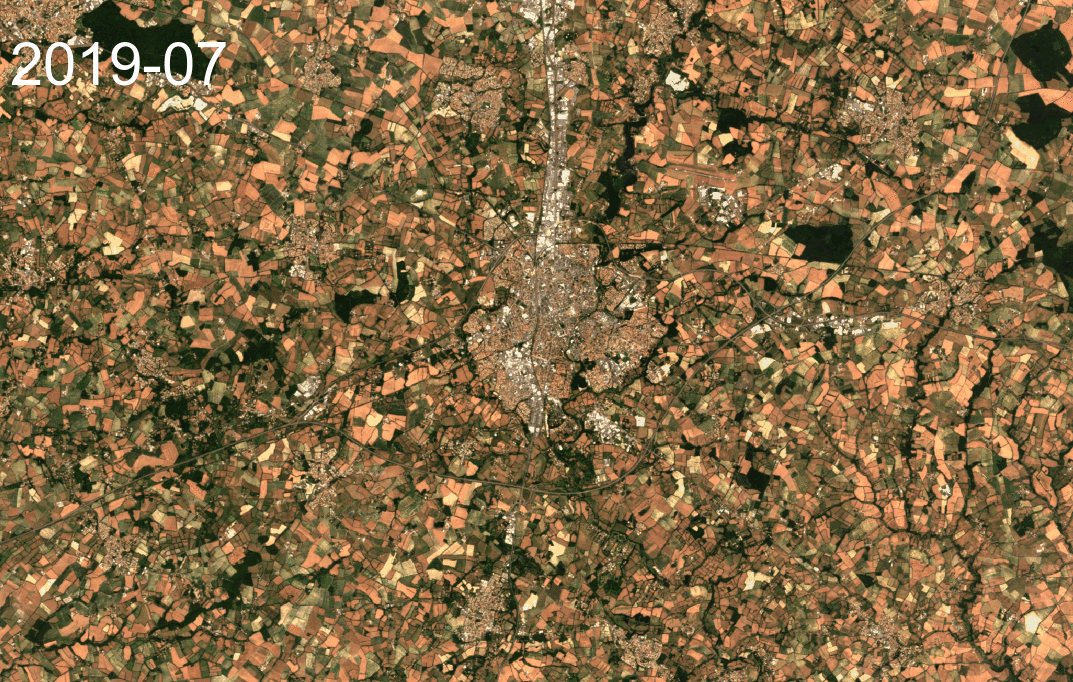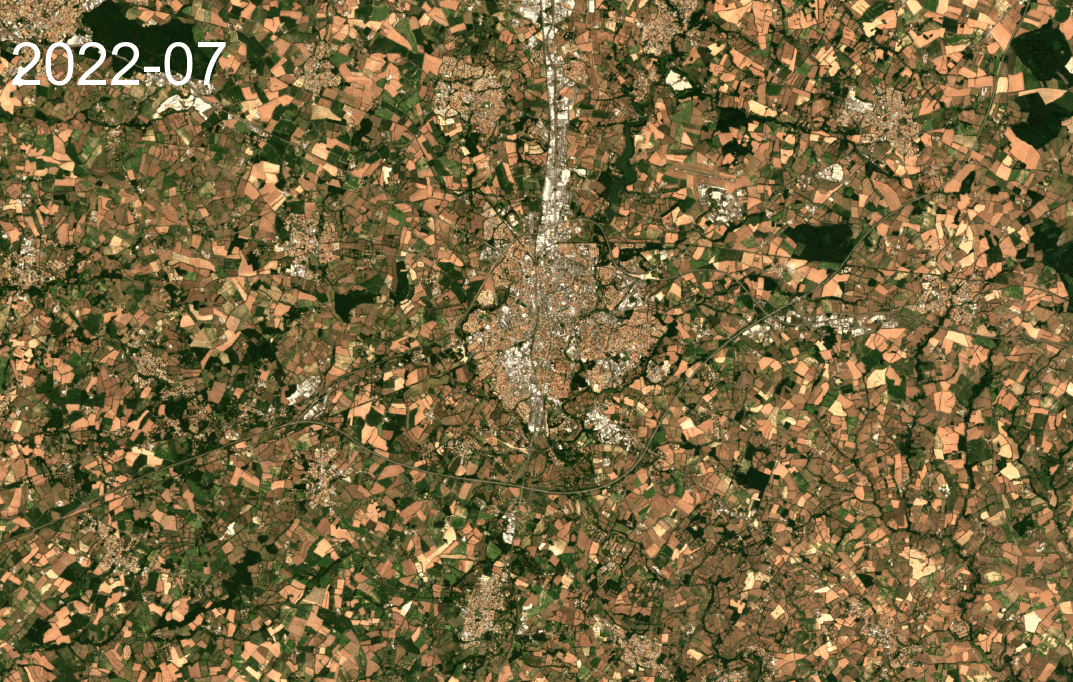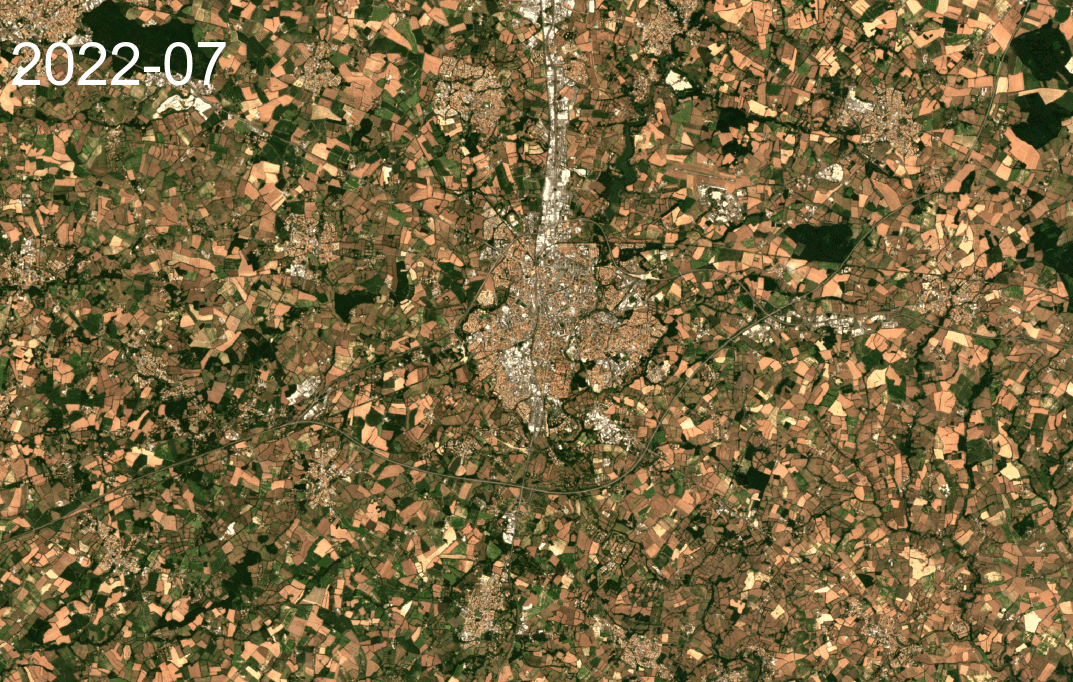
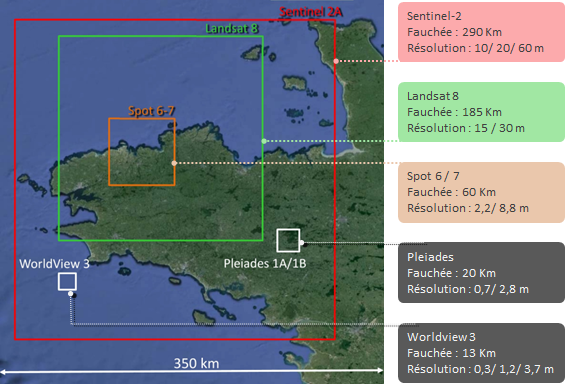
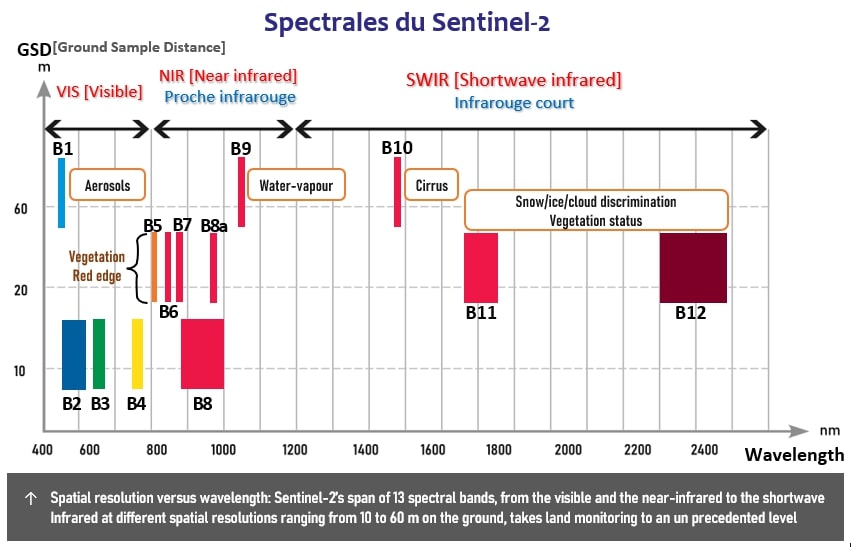
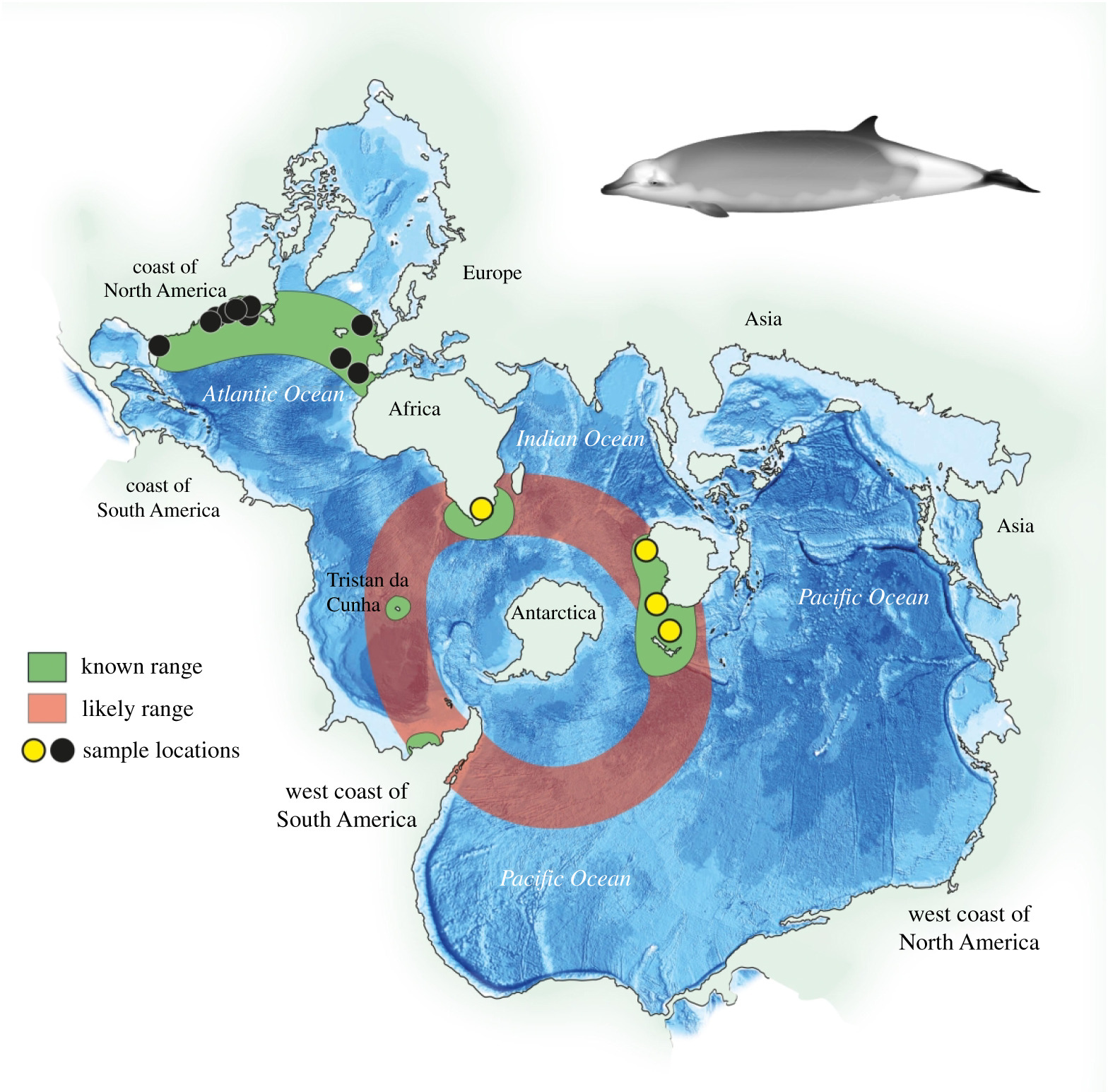
    Cette initiation vous permet d'avoir des notions basiques autour des données géospatiales : données vectorielles et matricielles (aussi appelées raster), formats courants et applications. Sont aussi évoqués des programmes de satellites d'observation et de surveillance de la Terre, la technologie LiDAR et les modèles MNT et MNE (Modèle Numérique du Terrain et d’Élévation). Enfin un diagramme évoque quelques pistes  pour trouver les données géospatiales en accès libre.

    Objectifs
    • Connaître les bases des données géospatiales
    • Comprendre les types de données géospatiales et leurs applications
    • Connaitre les principales plateformes des données géospatiales
    Ce cours est en libre accès !

    Aucune création de compte ou d'inscription n'est nécessaire, toutefois vous ne pourrez le parcourir qu'en lecture seule.

    Pour participer aux activités (exercices, forum...), vous devez vous inscrire au cours

    S'inscrire au cours

    • Auteur(s) / Formateur(s): Nicolas Roelandt - Université Gustave Eiffel, Marion Maisonobe - CNRS-Geographie-Cité
      Production cours: Olivier Lu - Urfist Lyon, Viet Jeannaud - Fondation Callisto
      Public cible: toute personne souhaitant s'initier aux données géospatiales.
      Date de publication: 21 juin 2024
      Durée estimée: 1 heure 30
      Prérequis: aucun
      Licence: CC BY-NC-SA
      Citation: N. ROELANDT, M. MAISONOBE and O. Lu, V. Jeannaud, “Gérer les données géospatiales" Callisto Formation, 2024.
      DOI: https://doi.org/10.60538/comprendre-data-geo
      Open badge: Non
      Nombre d'inscrits: 13
      Catalogue: Non


  • Replier Déplier

    1. Qu'est-ce qu'une donnée géospatiale ?

    Temps de lecture : 7min

    • Nicolas Roelandt, Marion Maisonobe. Callisto. (2024, 6 mars). Qu'est-ce qu'une donnée géospatiale ?. [Vidéo]. Canal-U. https://doi.org/10.60527/jrfd-bg90. (Consultée le 18 mars 2024)

    • Une donnée géospatiale est une information qu'il est possible de situer à la surface du globe terrestre.

      On retrouvera indifféremment tous ces termes dans la littérature :

      •  données localisées ou géolocalisées
      •  données géographiques
      •  données spatiales ou géospatiales 
      Animation de la rotation de la Terre.
      NASA/EPIC, edit by Tdadamemd, Public domain, via Wikimedia Commons

      Néanmoins, les spécialistes ont plutôt tendance à utiliser les termes "données géolocalisées" et "données géospatiales".

      Désignation : 

      • Géo : la Terre 
      • Locus : le lieu
      • Espace : étendue indéfinie

    • Comment définit-on une localisation ?

      Il y a plusieurs façons de définir une localisation :

      Exemple de coordonnées u et v sur une sphère.
      Maschen, CC0, via Wikimedia Commons
      En coordonnées sur la sphère

      Il est possible de déterminer la position d'un objet par la localisation avec des coordonnées u et v sur la sphère, contenue dans un repère XYZ.

      C'est ce système qui est utilisé pour la navigation maritime ou aérienne, avec des angles formés entre la position de l'objet considéré, le centre de gravité de la terre et l'Équateur ou le méridien de Greenwich. Cette méthode a été démocratisée par le GPS qui équipe à présent nos voitures et nos téléphones portables.

      Exemple de coordonnées u et v sur un plan.
      Maschen, CC0, via Wikimedia Commons
      En coordonnées sur le plan

      Il est aussi possible de déterminer la position d'un objet sur le plan, dans le cas de la lecture d'une carte routière ou topographique, avec des coordonnées en XY, et parfois l'altimétrie Z.

    • Enveloppe affichant une adresse postale.
      Steve Stuck, Public domain, via Wikimedia Commons
      Avec une adresse postale

      Il est possible de géolocaliser certains éléments tels que des personnes ou des bâtiments par exemple à l'aide d'une adresse postale.

      L'adresse postale est couramment utilisée par le grand public mais présente des inconvénients qui rendent parfois complexe sa conversion en coordonnées géographiques (procédé appelé géocodage, voir ci-dessous).

      Personne réalisant un quadrillage de la surface d'un site archéologique à l'aide de cordes et de piquets.
      Emily Brouwer (Mount Rainier National Park), CC-BY-2.0 via Wikimedia Commons
      Par rapport à un point connu

      Lors d'une fouille archéologique par exemple, un quadrillage est réalisé sur tout le chantier. La position de chaque maille est relevée et en mesurant les distances séparant l'objet du quadrillage, il est possible de le repérer sur la grille.

      Les mesures seront alors faites en système local, ce dernier pourra être raccordé à un système de coordonnées ultérieurement à l'aide de points connus en coordonnées.

    • Informations géographiques

      Ces informations relevées sont "analogiques", c’est-à-dire qu'elles sont réelles mais nécessitent deux points d’attention pour les exploiter : les métadonnées et la modélisation.

      Les métadonnées

      Par exemple, dans le cas d'une fouille archéologique, les archéologues relèvent différentes métadonnées telles que :

      • le contexte des fouilles,
      • les méthodes utilisées pour relever les données,
      • la localisation,
      • le type d'information.


      Toutes ces informations sont des métadonnées. La localisation (les coordonnées) est une métadonnée.

      Les données seules ont peu de sens ! Sans les métadonnées, les données n'auront que peu de valeur car elles sont difficilement exploitables.


      La modélisation

      Pour pouvoir utiliser toutes ces données et métadonnées dans un système d'information géographique (SIG), il est nécessaire de les numériser, puisque les systèmes d'information sont des systèmes numériques.

      Cette étape de modélisation est importante car elle permet :

      • de simplifier l'information,
      • de la quantifier (c'est-à-dire de la faire rentrer dans des échelles de valeurs qui permettent la comparaison entre plusieurs relevés),
      • de faire des regroupements thématiques (ce qui nous permettra peut-être de constituer des couches contenant des objets similaires),
      • et de faire correspondre cette information à un modèle de données standardisé qui permettra ultérieurement la lecture et les échanges de données.
      Jørgen Stamp, CC BY 2.5 DK, via Wikimedia Commons

    • Comment peut-on localiser une information géographique ?

      Par mesure directe

      À l'aide d'un GPS ou d'un tachéomètre par exemple.

      Exemple d'un récepteur GNSS monté sur une canne.

      Exemple d'un récepteur GNSS monté sur une canne, Patsy Lynch, Public domain, via Wikimedia Commons
      Par géocodage

      En relevant une adresse : cette information sera géocodée par la suite, c’est-à-dire convertie en coordonnées géographiques. Par exemple, en France, le site adresses.data.gouv.fr permet de passer d'une adresse à des coordonnées géographiques.

      Géolocalisation de la Pyramide du Louvre sur adresse.data.gouv.fr.
      ex. Pyramide du Louvre / adresse.data.gouv.fr]
      Par jointure

      Il est aussi possible de faire une jointure entre entités géographiques qui partagent une nomenclature commune. Par exemple, si le travail se fait à l'échelle de la commune et que les données sont liées aux codes Insee des communes étudiées, il est possible de joindre les données relevées sous forme de table avec les données géographiques de ces communes, tel que les contours communaux ou la position des chef-lieux.

      Illustration d'une table de jointure à l'aide du code INSEE.
      Nicolas Roelandt, Univ. Eiffel. Domaine public

    • Deux types d'information géographique

      L’information géographique peut être de deux types :

      Information discrète

      Ce sont des phénomènes que l'on peut qualifier de "finis". Par exemple sur l'image en bas, les bâtiments ont un contour bien précis.

      Carte affichant une information discrète : les bâtiments.
      Bartenev, Public domain, via Wikimedia Commons
      Information continue

      Ce sont des phénomènes dont le début ou la fin ne pourront pas être délimitées précisément. C'est le cas par exemple pour les mesures physiques comme la température ou les quantités de polluants atmosphériques, comme le montre la figure ci-dessous.

      Carte montrant une information continue : la densité de microplastiques dans les mers et océans.

      Eriksen, Marcus; Reisser, Julia; Galgani, Francois; Moore, Charles; Ryan, Peter; Carson, Hank; Thiel, Martin, CC BY-SA 4.0, via Wikimedia Commons
      Comment mesurer ces phénomènes ?

      Ils peuvent être mesurés :

      • soit de manière physique (de manière directe avec un capteur sur place ou de manière indirecte à l’aide d’un satellite).
      • soit par le biais d'un inventaire : en se déplaçant sur le site étudié et en réalisant un inventaire botanique ou faunistique.
      • soit encore, par le biais de réponses à des questionnaires.

    • Les deux modèles les plus courants

      Pour être exploitable dans un SIG, l'information spatiale doit correspondre à des modèles de données propres au domaine.

      Les deux modèles les plus courants, et les plus fréquemment utilisés, sont :

      Les données vectorielles

      Les données vectorielles sont ici illustrées par les points, lignes et polygones.

      Représentation de données vectorielles dans un SIG.
      F Lamiot d'après [1] (GNUFDL), CC BY-SA 3.0, via Wikimedia Commons
      Les données raster

      Les données raster sont proches des photographies numériques où chaque pixel de l'image porte une information.

      Représentation de données raster dans un SIG.
      Source : U.S. Government Accountability Office - Flickr

      D'autres modèles de données existent mais sont d'usage moins courant tels que les modèles topologiques ou les réseaux ou graphes.

  • Replier Déplier

    2. Types de données géospatiales

    Temps de lecture : 15min

    • Nicolas Roelandt, Marion Maisonobe. Callisto. (2024, 18 mars). Type de données géospatiales. [Vidéo]. Canal-U. https://doi.org/10.60527/y6fs-0v50. (Consultée le 18 mars 2024)

    • Comme nous avons pu le voir dans la section précédente, l’information mesurée sur le terrain doit être numérisée afin de pouvoir être stockée et exploitée par des ordinateurs.

      Il existe deux grandes familles de données qui ont chacune leurs particularités et leurs usages:

      • Les données raster constituées de grilles de pixel dont chaque cellule est porteuse d’une information.
      • Les données vectorielles constituées de points, lignes ou polygones dont les coordonnées des sommets sont connus et auxquels de l’information est attachée.
      Couches Raster et vectorielle
      Johannes Rössel, CC BY-SA 3.0, via Wikimedia Commons

      Selon les besoins, le (ou la) géomaticien(ne) peut utiliser des données vectorielles ou des données raster. Il est fréquent de manipuler des données de plusieurs types. Il existe également des formats de données géospatiales répondre à des besoins particuliers qui diffèrent de ces deux grandes familles.

    • Données vectorielles

      Les données vectorielles sont adaptées pour des phénomènes ponctuels ou discrets tels que des points d’intérêts, des contours administratifs ou les axes de communication. Elles associent à chaque entité (Feature) une forme (shape) dont le (ou les) sommet(s) est connu en coordonnées et des données sous forme de table.

      Forme Géométrie Modèle Simple Features Modèle OpenStreetMap

      Les points n’ont pas de dimensions et leurs coordonnées sont connus (latitude/longitude ou X/Y selon le système de référence de coordonnées).       		Sommet (vertex) Point Noeud (node)

      Les lignes (ou polylignes) sont constituées de points dans un ordre défini. Les points forment les sommets de la polyligne. Il est possible de calculer la longueur d’une polyligne.      		 Arête (edge) Ligne (Linestring) Way

      Un polygone est une polyligne fermée, c’est-à-dire que le point de départ et le point d’arrivée ont les mêmes coordonnées. Les sommets du polygone est constitués de points. Il est possible de calculer son périmètre et sa surface.      		 Face Polygone (Polygon) Closed way


      Il est possible de modifier des données vectorielles en les découpant, en ajoutant ou supprimant des sommets. On peut personnaliser l'affichage des données vectorielles en faisant varier l’épaisseur des traits, les couleurs, etc.

      Les formats les plus courants sont le shapefile (.shp), le Geopackage (.gpkg), le GeoJSON (.json) ou encore le csv. Ces formats implémentent le modèle Simple Feature Access, un standard défini par l’Open Geospatial Consortium.

      Le projet OpenStreetMap utilise son propre modèle basé sur le XML, de nombreux outils permettent de convertir ces données vers le modèle Simple Feature Access. Le KML, un autre format basé sur du XML, a été popularisé par l’outil Google Earth.

    • OpenStreetMap est un projet collaboratif mondial de constitution d'une base de données géographiques libre. Les données sont collectées par les contributeurs et leur licence libre permet leur réutilisation dans des outils SIG, dans des applications mobiles ou sous forme de fonds de carte. À l'instar de Wikipédia, tout le monde peut y contribuer et le projet permet de pallier au manque de données géographiques de référence à certains endroits ou sur certaines thématiques.

    • Données raster

      Les données raster sont bien adaptées pour l’étude de la variation de phénomènes continus (température de l’eau, altimétrie, enneigement, mode d’occupation des sols, etc.) sur des grandes surfaces. Les exemples les plus fréquents sont les images aériennes ou satellites, les mode d’occupation des sols ou les modèles numériques de terrain/ d’élévation.

      Voir légende
      Exemple de suivi d'un phénomène continu. Source : Sécheresse continentale 2022, CESBIO

      L’utilisation de données raster peut servir dans plusieurs domaines :

      • mesure d'impact  et évaluation des risques (sécheresse, incendie) ;
      • suivi de la déforestation ou de la fonte des glaces ;
      • détection et suivi de pollutions.

      Les données raster sont des grilles régulières constituées de cellules de taille identique dont la position est connue. Chaque cellule porte une information, par exemple l’altimétrie ou la réflectance dans une certaine longueur d’onde du spectre électromagnétique.

    • Caractéristiques importantes pour décrire les données raster

      Une image raster est définie par plusieurs éléments qui vous sont présentés ci-dessous.


      Résolution spatiale

      La résolution spatiale correspond à la taille sur le terrain d’un pixel. Par exemple, pour une image prise par un satellite Sentinel-2, la résolution spatiale dans le visible est de 10 mètres. C’est-à-dire qu’un pixel d’une image correspond à un carré de 10 mètres par 10 mètres au sol.

      Voir légende
      Comparaison de différentes résolutions spatiales. Source : applisat.fr


      Résolution temporelle

      La résolution temporelle est le temps entre deux prises de vues. Pour les satellites de la constellation Sentinel-2, la résolution temporelle est de 5 jours. C’est-à-dire qu’un endroit sera survolé tous les 5 jours par un satellite de cette constellation, ce qui est très régulier et permet de se rendre compte rapidement des changements (inondations, incendies).

      Voir légende
      L'évolution de la banquise du pôle nord entre 1979 et 2007. Source : National Snow and Ice Data Center


      Fauchée

      La fauchée est la largeur de la prise de vue. Pour Sentinel-2, elle est de 290 km alors que pour Landsat-8 elle est de 185 km. Les fauchées étant de plus en plus grandes et les capteurs de plus en plus précis, les images sont de plus en plus volumineuses, atteignant plusieurs giga octets.

      Voir légende

      Comparaison de différentes fauchées. Source : https://www.un-autre-regard-sur-la-terre.org/


      Résolution spectrale / Bandes

      La résolution spectrale correspond à la finesse des canaux du spectre électro-magnétique que le capteur enregistrera. En effet, certaines longueurs d’ondes du spectre électromagnétique sont absorbées par l’atmosphère terrestre et ne sont donc pas visibles depuis l’espace. Lors de la conception du capteur, les bandes correspondant à une certaine fraction du spectre électromagnétique sont sélectionnées en fonction des applications recherchées. Ces bandes peuvent ensuite être combinées pour la création de compositions colorées ou le calcul d’indices (santé de la végétation, détection d’incendies, etc.).

      Ainsi les images issues du programme Sentinel-2 disposent de 12 bandes:

      • B1 : pour la détection des aérosols
      • B2 (bleu), B3 (vert) et B4 (rouge) pour les images en lumière visible
      • B5 à B8a dans les rouges et proche-infrarouge pour l’étude de la végétation
      • B9 : détection de la vapeur d’eau dans l’atmosphère
      • B10 : détection des nuages
      • B11 et B12 : différenciation entre la neige, la glace et les nuages
      Voir légende
      Bandes spectrales de Sentinel-2 - Source : European Space Agency


      Les bandes occupent une largeur différente du spectre électromagnétique. Ainsi les bandes B5 et B6 couvrent une bande de 15 et 13 nanomètres respectivement, alors que B12 couvre 184 nanomètres. C’est cette largeur qui est appelée résolution spectrale.

      Chaque image sera composée d'une ou plusieurs bandes. Les bandes pourront être stockées dans un seul fichier ou il peut y avoir un fichier par bande.

      Les formats les plus courants sont :

      • le geoTIFF (.TIFF),
      • l’ESRI ASCII (.ASC)
      • le .XYZ
    • Impact des choix de plateforme et de capteur sur la qualité des données raster

      Le choix de la plateforme qui portera le capteur, que ce soit un satellite, un avion ou un drone, aura un impact sur la résolution temporelle et la fauchée. Le capteur utilisé aura un impact sur la résolution spectrale (par exemple un satellite peut enregistrer des images en RGB comme un appareil photo mais un appareil photo ne fournira pas d’information sur les bandes infra-rouge). En général, un capteur est développé pour un type de plateforme particulier.

      S'il est possible d’accéder aux images brutes, l’usage de produits pré-traités peut être intéressant (gain de temps, moins de risque d’erreurs ou d’oublis, etc.), ces produits corrigeront certains défauts liés à la prise de vue, aux perturbations atmosphériques ou proposerons des indices pré-calculés (sécheresse, hauteur des lacs et cours d’eau, occupation des sols, etc.).

      Le choix d’un produit raster dépendra des paramètres définis pour le projet: est-ce que la résolution temporelle est plus importante que la résolution spatiale ? Quelles longueurs d’ondes seront nécessaires ? Existe-t-il des produits pré-traités ? Sinon quels traitements seront nécessaires ?

      Par exemple, si on devait la comparer aux données SENTINEL-2, la BD ORTHO de l’IGN a une grande résolution spatiale (20 cm) mais une faible résolution temporelle, un département n’est survolé que tous les 3 ou 4 ans et ne rendra compte que des changements sur le temps long (artificialisation des sols, assèchement des zones humides, fonte de glacier). La résolution spectrale de la BD ORTHO est également réduite car les bandes disponibles sont la lumière visible (Rouge, Vert, Bleu) et l’infrarouge soit 4 bandes.

      Ces deux sources de données sont de grande qualité, l'un n'est pas meilleure que l'autre, mais il conviendra de choisir la plus adaptée au besoin visé.

    • Autres types de données géospatiales

      Il existe des formats spécifiques à certains usages qui ne sont pas toujours exploitables directement dans un SIG et/ou nécessitent l’utilisation d’extensions dédiées. C’est le cas des nuages de points LiDAR (.LAS,.LAZ,.XYZ) ou des données naturalistes (NetCDF, pour lequel une initiation est disponible ici, .GRID, .HDF). On peut ranger dans cette catégorie les données issues de la Conception Assistée par Ordinateur (.DWG,.DXF, etc.) qui se rapprocheront des fichiers vectoriels mais sans avoir de données tabulaires associées.

      Les données GPS sont souvent fournis par les appareils au format GPX (GPS eXchange Format). Il s’agit d’un ensemble de points dont certaines informations sont connues (position, altitude, horodatage) mais qu’il faudra généralement enrichir par la suite.

  • Replier Déplier

    3. Où trouver des données géospatiales ?

    Temps de lecture : 5min

  • Replier Déplier

    4. Système de référence de coordonnées et projections

    • Nous avons vu qu'un élément observé peut être positionné à la surface de la Terre à l'aide de coordonnées. Il s'agit souvent d'un doublet (latitude/longitude; est/nord) ou d'un triplet (latitude/longitude/hauteur ellipsoïdale; est/nord/altitude).

      Pour pouvoir les exploiter, il faut savoir dans quel système de référence de coordonnées elles sont exprimées. C'est une métadonnée d'importance.

      Il existe deux grands types:  

      • les systèmes géodésiques (aussi appelés systèmes de référence de coordonnées géographiques)
      • les systèmes de référence cartographiques (aussi appelés projections)

      La vidéo ci-dessous présente en 3 minutes les problématiques liées aux systèmes de référence et plus particulièrement les projections cartographiques.

    • Pourquoi existe-t-il deux systèmes ?

      La forme de la Terre se rapproche d'une sphère aplatie aux pôles, il est simple de localiser un point à sa surface à l'aide d'angles. Ainsi la latitude était mesurée avec précision dès l'Antiquité. La mesure de la longitude devra attendre les progrès de l'horlogerie aux XVIIe et XVIIIe siècles. C'est un système encore couramment utilisé pour la navigation aérienne ou maritime et par les systèmes GNSS. Mais il n'est pas pratique de mesurer une distance ou une surface sur un globe. C'est plus commode de faire des mesures sur une surface plane posée sur une table. Une carte sur du papier ou du vélin peut être roulée ou pliée, ce qui la rend bien plus pratique qu'une mappemonde. Pour créer une carte, il est nécessaire de projeter la sphère (systèmes géodésiques) sur le plan (systèmes projetés), c'est pourquoi on parle de projection. Pour passer d'un système de référence de coordonnées (géographique ou non) à un autre, on parlera d'une transformation. Les deux types de systèmes coexistent encore à l'heure actuelle et les ordinateurs permettent de passer de l'un à l'autre très simplement.

    • Systèmes géodésiques

      Il s'agit de systèmes où les coordonnées (latitude et longitude) sont des angles formés entre le centre de la Terre, l'Équateur et le premier méridien (ou méridien  de Greenwich). 

      Ces angles sont exprimés en degrés, minutes, secondes ou en degrés décimaux. 

      Ces points sont rattachés à un ellipsoïde de révolution, similaire à une sphère aplatie aux pôles, chargé d'approximer la surface terrestre. 

      Une troisième coordonnée, la hauteur ellipsoïdale est la différence entre le point considéré et l'ellipsoïde. Il ne s'agit pas d'une altitude, elle peut différer de plusieurs dizaines de mètres.

      The original uploader was Carlo denis at French Wikipedia., CC BY-SA 3.0, via Wikimedia Commons

      Les systèmes de navigation par satellites utilisent un système géodésique, c'est le cas du GPS américain qui repose sur le WGS 84.

    • Systèmes cartographiques (aussi appelés projections)

      Les systèmes de coordonnées projetées permettent la représentation de points situés à la surface terrestre sur une surface plane. 

      Cette opération, appelée transformation, engendre des déformations. Le travail du cartographe est de choisir la plus adaptée, selon que la carte devra préserver les angles, les distances, les surfaces ou rien de tout cela.

      Projections conformes

      Les projections conformes préservent les angles, facilitant la navigation entre deux points. C'est le cas de la projection Transverse universelle de Mercator (Universal Transverse Mercator ou UTM) par exemple. Cette projection est encore très utilisée puisqu'une variante dédiée aux applications cartographiques web a été créée, la projection Web Mercator. Bien qu'omniprésente sur les services de cartographies en ligne tels qu'OpenStreetMap ou Google Maps, elle n'est pas exempte des défauts de sa grande sœur (voir ci-dessous le passage sur la visualisation des déformations induites par la projection Mercator).

      Voir légende.
      Exemple de projection Web Mercator. Strebe, CC BY-SA 4.0, via Wikimedia Commons
      Voir la légende.
      Projection de Peters de la Terre. Mdf, Public domain, via Wikimedia Commons
      Projections équivalentes

      Les projections équivalentes préservent les surfaces, ce qui les rendent utiles pour des comparaisons de densité par exemple. Ainsi, la projection de Gall-Peters montre un Groënland 14 fois plus petit que le continent africain, contrairement à la projection UTM, ce qui correspond à la réalité.

      Projections équidistantes

      Les projections équidistantes préservent les distances mais ne conservent ni les angles ni les surfaces.

      Description dans la légende ci-dessous.
      Projection équirectangulaire de la Terre. NASA
    • Visualiser les déformations avec les indicatrices de Tissot

      Comme nous l'avons vu précédemment, toutes les projections déforment la réalité. Il peut être intéressant de visualiser ces déformations pour mieux s'en rendre compte. C'est ce que permettent les indicatrices de Tissot.

      Les deux images ci-dessous représentent la même chose : des surfaces appelées indicatrices de Tissot. Elles servent à visualiser les déformations produites par une projection. 

      L'image de gauche représente ces indicatrices réparties régulièrement autour du globe. Tous les cercles font la même taille. L'image de droite reprend les mêmes cercles mais sur une carte utilisant la projection universelle transverse de Mercator: les cercles grossissent plus leur latitude augmente (vers les pôles).

      World Map (Canvas) with Tissot’s Indicatrices - Sorami Hisamoto, Observable

      La NASA propose de visualiser les déformations de différentes projections dans cette vidéo de 47 secondes.

      Map Projections Morph - NASA Scientific Visualization Studio, on YouTube

    • Pourquoi la gestion des systèmes de référence de coordonnées peut être problématique ?

      La gestion des systèmes de référence de coordonnées (souvent abrégé avec l'acronyme anglophone CRS) pose généralement des problèmes aux personnes confrontées pour la première fois à des données géographiques et même des utilisateurs chevronnés pourront se faire avoir de temps en temps.

      Croiser des données géographiques ayant des CRS différents (par exemple WGS 84 d'un côté et RGF93/Lambert93 de l'autre) pourra, au mieux, ne retourner aucun résultat ou, dans le pire des cas, retourner un résultat erroné. L'ordinateur exécutera l'algorithme sans se poser de questions, c'est à l'opérateur (c'est-à-dire vous) de prêter attention aux CRS des couches utilisées.

      Les algorithmes fonctionnant avec des distances (ou calculant des surfaces) sont souvent codés pour fonctionner pour des systèmes de coordonnées projetés. Par exemple, un algorithme calculant la distance entre deux points utilisera par défaut la distance euclidienne (le théorème de Pythagore, vous vous souvenez ?) car c'est rapide et peu couteux à réaliser. Par contre, pour des données dans un système géodésique, situant des objets à la surface de la Terre, il faut calculer la distance orthodromique (ou distance du grand cercle). Cette méthode nécessitant de calculer des sinus et des cosinus, il est alors préférable de transformer les coordonnées dans un système de coordonnées planes avant d'effectuer des calculs de distance. La puissance de calcul des ordinateurs ayant fortement progressée, il est possible de calculer la distance orthodromique mais il convient de choisir un algorithme adapté.

    • Comment choisir une projection ?

      Nous avons vu que la transformation de coordonnées géographiques vers un système de référence de coordonnées projetées entraine une déformation. Il convient alors de choisir une projection adaptée au besoin et à la zone représentée.



      Quel est le besoin ?
      • A-t-on besoin de mesurer des angles ? Une projection conforme est préférable.
      • Des distances ? Une projection équidistante sera à privilégier.
      • De calculer des aires ou des densités ? L'utilisation d'une projection équivalente est recommandée.


      Quelle zone est représentée ?
      • Pour les zones équatoriales et tropicales, les projections cylindriques comme la projection UTM sont adaptées.
      • Pour les zones de latitudes moyennes (France/Europe par exemple), les projections coniques sont fréquemment utilisées.
      • Pour les hautes latitudes (Pôles et cercle arctique), il est préférable d'utiliser une projection azimutale.


      Une bonne piste pour trouver une projection adaptée à une zone d'études est de regarder les projections légales. Par exemple, l'IGN fournit des projections légales pour la France métropolitaines et les départements, régions et collectivités d'outre-mer. Ces projections planes légales sont définies dans l'article 3 de l'Arrêté du 5 mars 2019 portant application du décret n° 2000-1276 du 26 décembre 2000.

    • Pour des raisons historiques, esthétiques ou de représentation, d'autres projections peuvent être choisies (projections de Fuller, de Bonne ou Goode par exemple).

      Un cartographe qui travaille sur les océans mondiaux saura utiliser à son avantage la superbe projection de Spilhaus.


      Description ci-dessous.
      Carte d'échantillonnage de baleines à bec utilisant la projection de Splihaus.
      Source: Vivian Ward, CC BY-SA 4.0, via Wikimedia Commons
    • Catalogues

      Les déformations locales de la surface terrestre, les progrès de la technique et d'autres facteurs font que plusieurs milliers de systèmes de références de coordonnées existent. Pour s'y retrouver, des catalogues (ou registres) ont été créés.

      Ces catalogues associent la définition d'un système de référence de coordonnées et un code.

      Ce code est constitué en deux parties séparées par deux points :, à gauche la référence du catalogue (EPSG,IGNF,ESRI) et à droite, le code de la projection dans ce catalogue (respectivement 2154, LAMB93, 102110).

      Ainsi EPSG:2154, IGNF:LAMB93 et ESRI:102110 référencent tous trois la projection RGF93/Lambert93 mais dans 3 catalogues différents.

      Par exemple, la définition WGS84 est associé au code EPSG:4326 alors que sa description en Well-Known Text est la suivante:

                GEOGCRS["WGS 84",
                    ENSEMBLE["World Geodetic System 1984 ensemble",
                        MEMBER["World Geodetic System 1984 (Transit)"],
                        MEMBER["World Geodetic System 1984 (G730)"],
                        MEMBER["World Geodetic System 1984 (G873)"],
                        MEMBER["World Geodetic System 1984 (G1150)"],
                        MEMBER["World Geodetic System 1984 (G1674)"],
                        MEMBER["World Geodetic System 1984 (G1762)"],
                        MEMBER["World Geodetic System 1984 (G2139)"],
                        ELLIPSOID["WGS 84",6378137,298.257223563,
                            LENGTHUNIT["metre",1]],
                        ENSEMBLEACCURACY[2.0]],
                    PRIMEM["Greenwich",0,
                        ANGLEUNIT["degree",0.0174532925199433]],
                    CS[ellipsoidal,2],
                        AXIS["geodetic latitude (Lat)",north,
                            ORDER[1],
                            ANGLEUNIT["degree",0.0174532925199433]],
                        AXIS["geodetic longitude (Lon)",east,
                            ORDER[2],
                            ANGLEUNIT["degree",0.0174532925199433]],
                    USAGE[
                        SCOPE["Horizontal component of 3D system."],
                        AREA["World."],
                        BBOX[-90,-180,90,180]],
                    ID["EPSG",4326]]

       

      EPSG:4326 est plus court et facile à se rappeler, n'est-ce pas ?

      Une même projection pourra avoir plusieurs codes si elle est référencée dans plusieurs catalogues. Ainsi le RGF93/Lambert93 (projection légale en France métropolitaine) correspond aux codes EPSG:2154 et IGNF:LAMB93

      Les outils SIG permettent pour la plupart de transformer vos données d'un système à un autre. Choisissez la projection la plus adaptée à votre zone d'étude et à votre besoin et transformez toutes vos données dans ce système. À moins de travailler à l'échelle mondiale, il est recommandé de travailler avec des systèmes projetés.

      Important: pour croiser des données de manière géographique, il est primordial que les jeux de données soient dans le même système de référence.

      Dans l'exemple ci-dessous tiré de la fenêtre de sélection d'un système de référence de coordonnées de QGIS, il est possible de voir :

      • Dans l'encadré vert, la fenêtre de recherche d'un CRS, ici autour du Lambert93.
      • Dans l'encadré bleu, les CRS disponibles sont regroupés par familles (géocentriques, géographiques, projeté) et en sous-famille. Dans l'exemple, il est possible de voir les sous-familles de projection: Mercator, Orthographique, Lambert conique conforme, etc.
      • Dans l'encadré violet, la description textuelle du RGF93/Lambert93.
      • Dans l'encadré rouge, l'emprise du système de référence de coordonnées (dans l'exemple centré sur la France métropolitaine).

       

       

    • En résumé, pour éviter les écueils
      1. Choisir un système de coordonnées adapté :
        1. à la zone d'étude, à jour si possible
        2. au besoin: a-t-on besoin de calculer des distances ou des surfaces/densités ?
      2. Vérifier les CRS des jeux de données mobilisés et les transformer vers le CRS sélectionné si nécessaire. Tous les logiciels SIG proposent des outils de transformation qui permettent de passer d'un CRS à un autre.
      3. Avant d'utiliser un outil, essayer de savoir s'il fonctionne avec des coordonnées projetées (le cas général) ou non.

      Les sites Spatial Reference et espg.io permettent de rechercher des informations sur un CRS à partir de son code ou de son nom.

    • Systèmes de référence de coordonnées usuels


      France
      Zone Nom Code
      France métropolitaine Lambert-93 IGNF:RGF93LAMB93
      Coniques conformes zone 1 à 9 RGF93CC42 à RGF93CC50
      Antilles françaises Universal transverse Mercator fuseau 20 nord IGNF:RGAF09UTM20
      Guyane Universal transverse Mercator fuseau 22 nord IGNF:RGFG95UTM22
      La Réunion Universal transverse Mercator fuseau 40 sud IGNF:RGR92UTM40S
      Mayotte Universal transverse Mercator fuseau 38 sud IGNF:RGM04UTM38S
    • Europe
      ETRS89-extended / LAEA Europe : projection utilisée pour les données géographiques Eurostat de la Commission Européenne.
      Code EPSG:3035


      Monde

      WGS84: système de référence de coordonnées géographiques utilisés par le système GPS.
      Code EPSG:4326

      WGS 84 / Pseudo-Mercator -- Spherical Mercator: projection utilisée par les fonds de cartes web (OpenStreetMap, Google maps, etc.).
      Code ESPG:3857

  • Replier Déplier

    Pour aller plus loin

  • Replier Déplier

    Échanger sur le cours

    Un forum est à votre disposition pour toute question. Vous pouvez aussi nous aider à améliorer ce cours en donnant votre avis.

    • Forum
  • Replier Déplier

    Sur le même thème

    Cours: Rédiger un DMP pour sa thèse en biologie
    Cours: La question des données en Bio-Informatique
    Cours: La gestion des données de recherche en environnement
    Cours: Comprendre les données géographiques
    Cours: Ouvrir les données de recherche en informatique théorique : qu'a-t-on à y gagner ?
    Cours: Cohortes en santé : données ouvertes en imagerie médicale

    Autres suggestions

    Cours: Au-delà du secret statistique : comment accéder à des données confidentielles issues de la statistique publique ?
    Cours: netCDF, format de fichier interopérable pour la science ouverte
    Cours: Comment inscrire une recherche (action) participative respectueuse des principes FAIR ?
    Cours: Exemples d'entrepôts de données en SHS
    Cours: Étude de cas Économie-Gestion
    Cours: Droit de la concurrence : approche quantitative de jeux de données juridiques
    Cours: Humanités numériques : gérer ses données dans une équipe interdisciplinaire
    Cours: La diffusion des données de recherche en linguistique
    Cours: Langues minorisées à corpus restreint : partager pour survivre
    Cours: Le Plan de Gestion de Données pas à pas